(1)
MATHEMATICAL MODEL FOR CONTAMINATED
SOIL CLEAN UP
Rasheed R. Owain
King Abdulaziz City for Science and Technology
P O Box 6086
Riyadh - 11442, Saudi Arabia
M. Wacks
University of Arizona, Nuclear and Energy Division
Tucson 85721, USA
ABSTRACT
An ex-situ soil contamination cleanup technique is developed. The physical system which embodies a set of two-dimensional partial differential equations for underground water are solved. These equations, however, consist of water continuity equation. The surfactant and contaminant equations are coupled via Wilson s isotherm. The developed method is found to be very efficient and the results are consistent with a simple model, which is also solved numerically to validate the results.
Some cases are discussed, which have different operating and inlet and outlet conditions. Cases which have inlets and outlets at the same level are found to take longer time than those which have inlet and outlet at different levels for the contaminant to be cleaned up entirely.
INTRODUCTION
Contamination of the soil has rapidly become a major problem. Soil contamination by hazardous wastes has become a pervasive problem at waste sites with potentially serious consequences to those persons working or living near them[1]. In situ soil flushing technique is, however, not practical unless an impermeable soil layer is present the contaminant will seep to the uncontaminated surrounding areas. In this research an ex-situ soil cleanup is presented, the contaminated soil, however, has to be excavated and loaded into prefabricated rooms, these rooms are open from the top and have inlets and outlets, the water and the surfactants are injected at the inlet and the contaminated water is recovered at the outlet. The recovered water can be treated to remove the contaminants and reused. Finite difference methods are used to solve the two dimensional physical equations and the evaluated parameters are pressure, velocities, surfactant concentration, contaminant concentration. The surfactant and contaminant concentration are, however, evaluated as a function of time. In order to study the effect of dimensions, inlet parameters and inlet and outlet positions, some cases are discussed.
Clark and Mutch [2] in their survey of clean-up technologies have observed that all on-site management remedial alternatives are far less expensive than methods involving excavation. Ellis, et al.[3],carried out laboratory studies to develop an improved methodology applicable to the on-site treatment of organic chemical contaminated soil. Their studies showed that the use of the same water for repeated cycles precludes the generation of large volumes of waste leachate. Raghavan et al.[4] investigated the state of the art technologies for the extraction of contaminants from soil. He reported that the separation of the extractant from the soil and the regeneration of the extractant have not been successfully demonstrated for clay soils, but, above-ground extraction of organics and heavy metals is feasible from sandy soil containing very low levels of clay and humus fractions.
Wilson et al.[5] developed mathematical models to evaluate the feasibility of on-site vapor stripping for selected chemicals and site-specific environments. They found out that the removal rate is approximately inversely proportional to soil-moisture content. Gannon et al.[6] modified the model that was originally developed by Wilson et al. to include the effects of a gas-impervious cap on the velocity field of the moving soil gas. They found that the use of impermeable circular caps to direct soil gas flow could increase overall vapor stripping removal rates on the order of 50%.
Wilson et al.[7] extended their earlier model to examine the possible benefits of using passive vent wells to increase clean up rates. Contrary to their expectation, these do not generally seem to improve soil vapor stripping performance. Finally, Wilson and Clarke[8] concluded that although flushing is still very much in the developmental stage, it has the potential to reduce costs and environmental impact significantly in the clean up of hazardous waste sites.
MATHEMATICAL MODEL
When Darcy's law is written in a differential form, one gets the following relations[9]:
(1) |
(2) |
(3) |
where u, v and w are the velocities in the x, y and z directions respectively, b is the porosity, kx, ky and kz are the hydraulic conductivity's in the x, y and z direction respectively, h in the above equations can be replaced by P/g where P is the pressure and g is the volumetric weight of water
(4) |
(5) |
(6) |
and for water y may be assumed constant.
It is known that the conservation of mass equation is of the form
| (7) |
For water, density p may be assumed constant and equation(8) becomes
| (8) |
When equations (4),(5),and (6) are substituted into (8) one may get
| (9) |
The above equation is a second order linear partial differential equation and has only one unknown which is the pressure and can be solved numerically as will be shown later. However, when the pressure field is evaluated the velocities u, v, and w can be evaluated readily by solving equations (4) , (5)and (6).
The conservation equations of the contaminant and the surfactants are given by
Contaminant equation [10]:
| (10) |
Surfactant equation [10]:
| (11) |
The parameters in the above equation are defined as:
C= contaminant mass per unit volume of soil.
S= concentration of surfactants in the aqueous phase.
D= diffusion coefficient.
g= contaminant concentration solubilized and dissolved in the aqueous phase.
It has to be mentioned, in this research that the surfactant is assumed to be anionic. Since the water is assumed incompressible, equations (10) and (11) reduce to
| (12) |
| (13) |
Equations (12) and (14) are coupled and linked by Wilson's isotherem[11].
| (14) |
where Co, the contaminant solubility in pure water, Kd, mg/L contaminant per mg/L of surfactant, cmc, critical micelle concentration of surfactant, and C1/2 is the soil adsorption parameters. Equations (12), (13), and (14) are, however, solved after the velocity field has been established by equations (4) ,(5) ,and (6).
There are many useful methods to solve equation (9), however, splitting technique known as alternating direction implicit (ADI)[11] is implemented here. In this method a pseudo time term is added to the right hand side of equation (9) so that it becomes
(15) |
For simplicity, however, two dimensional flow is assumed and the last term in the above equation is omitted. Now the above equation can be written as
| (16) |
Where
| (17) |
Equation (12) and (13) can be reduced to the following
| (18) |
and
(19) |
The above two equations are solved using MacCormack's scheme which consists of a predictor corrector explicit levels [12].
When applying this scheme, the discretrized surfactant equation becomes
Predictor:
| (20) |
Corrector:
| (21) |
Similarly the contaminant equation also becomes
Predictor:
| (22) |
Corrector:
| (23) |
RESULTS AND DISCUSSION
The numerical procedure that was discussed in the above section is implemented for different geometries. It is assumed, however, that the contaminated soil is excavated and put inside prefabricated walls. These walls have one inlet for the water and the surfactant and outlet to drain the contaminated water, the advantages of this method over the in-situ soil cleanup are:
Some cases are discussed in this research which have either different inlet and outlet conditions or different dimensions presented in the following table.
| Parameter | Case No.1 | Case No.2 | Case No.3 |
| Length, m | 20 | 20 | 40 |
| Height, m | 20 | 20 | 40 |
| Inlet pressure head, m | 100 | 20 | 50 |
| Outlet pressure head, m | 0 | 0 | 40 |
| Inlet dimension, m | 2 | 2 | 2 |
| Outlet dimension, m | 2 | 2 | 2 |
The water is injected at first at the inlet until steady state is achieved and the velocity and pressure fields are established and the surfactant is injected at a constant rate at the inlet.
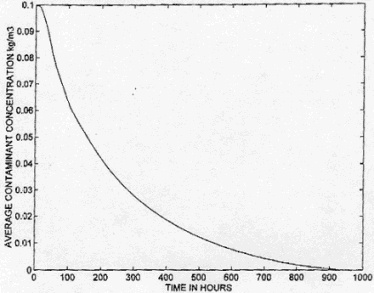
Figure 1. The Average Contaminant Concentration as a Function of Time for Case 3.
CONCLUSIONS
In this research, an ex-situ soil cleanup method was presented. The physical system which consists of partial differential equations was solved and tested. The results obtained in the previous chapter show that the method used in this research is powerful and converges to the steady state solution rapidly. The velocity field is, however, evaluated after solving the pressure equation which was solved implicitly and then solved explicitly to validate the results. The explicit method is very slow compared to the implication because of the stability condition. However, the implicit method is known as an alternating direction implicit (ADI) way found to be very fast and unconditionally stable. The pressure field obtained from the implicit method was compared to the results that were obtained from the explicit method and the results were found to be identical. The surfactant and contaminant equations were solved using two methods. The MacCormack explicit scheme was implemented to evaluate the surfactant concentration as a function of time. The contaminant equation was solved simultaneously with the surfactant equation using the Wilson coupling isotherm. To validate the results that were obtained from the MacCormack scheme, an explicit upwind scheme was implemented. The MacCormack scheme, however, has a stability range much more than that of the upwind scheme. However, the results obtained from both schemes are very similar. The advantages of this method over the in-situ methods are All the injected water can be recycled and used again.
Since all the injected water is recovered, this guarantees that the contamination will not seep to uncontaminated areas. Since no water is lost this also guarantees that the water will not go to areas where there is no contamination and this will accelerate the cleanup process. Because the soil is excavated it will be very easy to structure the soil so that the porosity, permeability, and other variables are known in advance. However, the main disadvantage of this method is the cost of the excavation, the confining walls and putting back the soil where it was taken from.