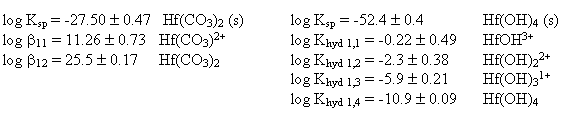
ENVIRONMENTAL BEHAVIOR OF HAFNIUM FOR THE
DISPOSAL OF WEAPONS-GRADE PLUTONIUM
G. Cerefice, M. Draye, K. L. Noyes, K. Czerwinski
Department of Nuclear Engineering, Massachusetts Institute of Technology
24-210, 77 Massachusetts Ave., Cambridge, MA 02139.
KCZER@MIT.EDU
ABSTRACT
Hafnium is one of the elements that has been considered for use as a neutron poison in the immobilization of Weapons-Grade Plutonium (WGPu). To examine its effectiveness as a neutron poison under repository-like conditions, it is first necessary to understand how the hafnium will behave in the environment. Through solubility experiments, the solubility and the first 2 stability constants for hafnium-carbonate were determined. Through dissolution and solubility experiments, the solubility and stability constants for hafnium-hydroxide were also determined. The constants determined in this work are:
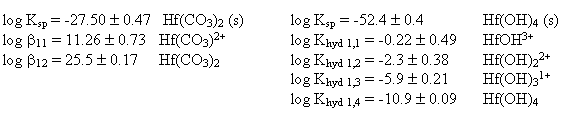
These constants, along with literature values for plutonium carbonate and hydroxide complexes, were then used to perform speciation and solubility limit calculations for hafnium and plutonium under conditions typical of those expected at Yucca Mountain.
INTRODUCTION
The current U.S. strategy for the disposition of surplus weapons-grade plutonium recovered from dismantled nuclear weapons calls for the development of two dispositioning options: burning the WGPu as fuel in commercial nuclear reactors and directly disposing of the WGPu in the high level waste repository in some immobilized form. The current formulation of the WGPu immobilization host phase consists primarily of pyrochlore with smaller amounts of hafnium-zirconolite, rutile, and brannerinte or perovskite. In this formulation, the zirconium is completely replaced by hafnium, uranium, plutonium, and gadolinium. The hafnium and gadolinium are present in molar amounts equal to that of the WGPu to serve as long-term criticality control element for the geological disposal of immobilized WGPu [1]. However, very little is known about the behavior of hafnium in the environment, particularly regarding its interaction with carbonates and hydroxides, both common environmental ligands.
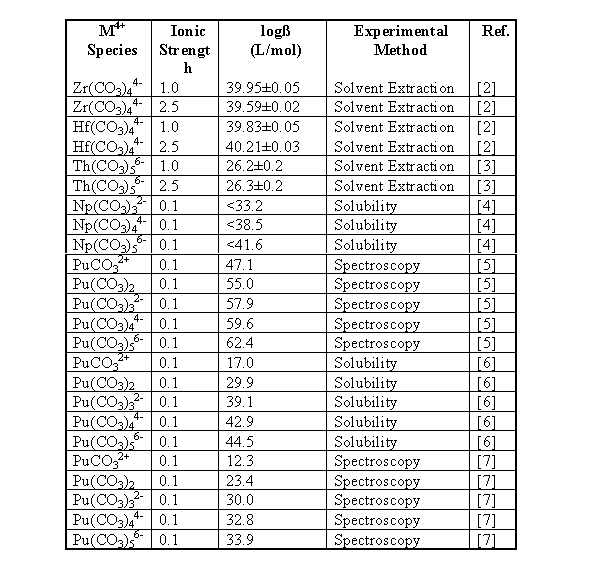
A review of the literature yielded the following stability and solubility constants for tetravalent metal carbonates (Table 1). A large variation in the stability constants is present. The large values for Pu carbonates indicate they would dominate under a wide range of conditions. However, laboratory experiments and environmental observations indicate the Pu(IV) carbonates are not as prominent as indicated by the large complexation constants [7]. This large variation in the stability constants, as well as the lack of data on hafnium complexation with carbonate, indicates a need to perform more experiments to evaluate important constants.
Table 1. Stability Constants of Some Tetravalent Metal Carbonates
This paper describes the initial results from work done to determine some of the thermodynamic constants that will govern the behavior of hafnium in the environment. The experimental section will describe the procedures used to determine the solubility and stability constants for the hafnium carbonate and hydroxide. The results of the experimental work, along with speciation and solubility limit calculations are presented. The experiments described in this work were performed at 0.1 M ionic strength. To determine the equilibrium constants at any other ionic strength, either the specific ion interaction theory (SIT) [11, 12] or the ion interaction equations of Pitzer [8,13] can be used.
EXPERIMENTAL
Materials
All chemicals and buffers were purchased from Aldrich. FTIR spectra were recorded on a 1600 Perkin-Elmer spectrophotometer. For the IR analysis, the Hf(CO3)2(s) was prepared in a KBr pellet in the range 4000-400 cm-1. The mass of all samples was determined using an OHAUSÒ Precision Plus Balance. The solution pH was measured with a ROSS-type combination electrode and Omega PHB-47 Microprocessor pH meter calibrated with buffer solutions. Some of the hafnium carbonate samples were filtered using a 5 ml syringe and a Cole-Parmer 0.45 m m PTFE filter. The Hf hydroxide samples were filtered using a 5 ml syringe and a Cole-Parmer 0.2 m m Cellulose Acetate filter.
Solid Phase Preparation
Hafnium carbonate and hydroxide solid phases were prepared. In a 50 mL round bottom flask placed in an ice bath, 20 mL of 0.1 M NaClO4 was slowly added to a fixed quantity of HfCl4 (s). To prepare the Hf(CO3)2 (s), 100% CO2 was bubbled through the solution while HfCl4 (s) was dissolved. The solution was then allowed to equilibrate for 20 hours. After the equilibration time, the solution was slowly adjusted to pH 4 by the addition of 0.05 M Na2CO3 over a period of three days. The solution was then allowed to stand for 1 week under 100% CO2 atmosphere. To prepare the Hf(OH)4 (s), the same procedure was used, except that 100% Ar gas was used instead of CO2, and a 0.1 M NaOH solution was used instead of a Na2CO3 solution to increase the system pH.
Solubility Experiments
To determine the solubility constant and stability constants for hafnium carbonate, a saturated system was prepared by dissolving Hf(CO3)2(s) in a 0.1 M NaClO4 solution under 100% CO2. The pH of the system was measured, and 5 mL of the supernatant solution was drawn off for analysis. The samples were stabilized by the addition of 100 m L of concentrated HNO3 and analyzed using ICP-AES. Some of the samples were filtered through a 0.45 m m filter before the nitric acid was added. After the 3 to 4 samples had been taken, the pH level was adjusted with Na2CO3 or HCl and the process repeated to determine a solubility curve. After the last sample at a given pH was taken, the removed volume was replaced with 0.1 M NaClO4 and allowed to come to equilibrium before being adjusted to the next pH level.
For the hafnium hydroxide solubility experiment, the procedure was similar to that used for the Hf carbonate solubility experiment, with the primary differences being that the saturated system was prepared using Hf(OH)4 (s) under 100% Ar. All of these samples were filtered through a 0.2 m m filter before being stabilized by the addition of 100 m L of concentrated HNO3.
Hf Hydrolysis Constant Estimation
In a 50 mL round bottom flask in an ice bath, 20 mL of DI water was slowly added to a measured quantity of HfCl4 (s). The HfCl4 was dissolved while 100% argon was bubbled through the solution. The solution was then allowed to equilibrate for 20 hours, after which the pH was measured. The change in pH of the resulting solution was due to the hydrolysis of Hf. Given that no precipitation occurs, the role of solubility can be ignored. Two equations can be written to describe the concentration of the different Hf species. From the hydrolysis reaction, the observed concentration of H+ is equal to the total amount of hydroxide complexed to Hf plus the initial H+ concentration, which is negligible in this case:
|
|
(1) |
The total amount of Hf in solution, [Hf]aq, can be written as:
|
|
(2) |
The hydrolysis constants are described by:
|
|
(3) |
The stability constants for the Hf hydroxide complexes are given by:
|
|
(4) |
Ligand Concentration
For these experiments, the ligand concentrations were determined from the measured pH of the system from the following equations. The aqueous carbonate ion concentration for a 0.1 M ionic strength solution was calculated at a given pH and CO2 partial pressure using equation 5, which was derived from the equilibrium expressions for the ![]() system [8].
system [8].
|
|
(5) |
The hydroxide ion concentration for the I = 0.1 M system was determined using equation 6. A hydrolysis product (Kw=) for a 0.1 M NaClO4 system of log KW = -13.79 was used for these calculations [8].
|
|
(6) |
Mass Balance Equations
From the definitions of the solubility constant (Eq. 7) and the stability constants, ß1x, (Eq. 8), along with a mass balance for the total hafnium in solution (Eq. 9), a relationship for the total Hf concentration in solution was derived (Eq. 10). The total hafnium concentration in solution is given by [Hf]aq in these equations, and the concentration of the free hafnium ion is given by [Hf4+].
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
From the definition of the solubility product for hafnium hydroxide (Eq. 11), along with a mass balance equation for hafnium (Eq. 12 ), and the definition of the stability constants (Eq. 4), it is possible to derive an equation for the solubility product given the stability constants and the hydroxide ion concentration (Eq. 14).
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
RESULTS
Hf Carbonate Solubility Experiment
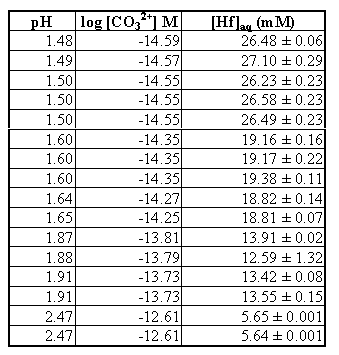
After allowing the system to equilibrate, a white precipitate was observed to be collecting on the lowest part of the round bottom flask. The precipitate was found to contain carbonate by IR spectroscopy (FTIR, (KBr): n = 1431 cm-1, 843 cm-1, 694 cm-1). We assumed that the solid was Hf(CO3)2 (s), but it could possibly be HfCO3(OH)2 (s). By comparing observed hafnium concentrations in both unfiltered samples and samples filtered with a 0.45 Fm filter, no colloidal species were found in the solution. The Hf carbonate solubility data is listed in Table 2.
From a least-squares fit of the data to equation 10, the following estimates of Ksp, ß11, and ß12 were obtained for a 0.1 M ionic strength hafnium carbonate system. For this curve fit, only the first 2 carbonato complexes were considered (x = 1-2 in equation 10), as the data obtained was only for low pH.
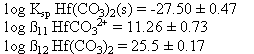
Table 2. Hafnium Carbonate Solubility Data (0.1 M NaClO4 System, 100% CO2)
Hf Hydrolysis Constant Estimation
In a 50 mL round bottom flask in an ice bath, 20 mL of DI water was slowly added to 1.224 g of HfCl4 (s). The HfCl4 dissolved in 10 minutes, during which time 100% argon was bubbled through the solution. At the end of the equilibrium time, no precipitate was observed and the solution stabilized at pH 0.80. Using these results, and initial estimate of the Hf hydrolysis constants can be obtained.
The different species from equations 1 and 2 were composed in terms of the hydrolysis constants (Eq. 3) and simultaneously solved. The resulting values are: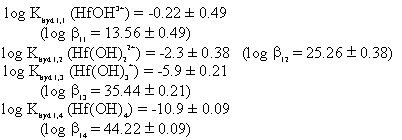
These values should only be taken as initial estimates, especially for the higher order hydrolysis species since they are not significant species in the pH examined. Additionally, the solution reading of pH 0.8 is below the normal response of the pH electrode. The stability constants are found through equation 4.
Hf Hydroxide Solubility Experiment
After equilibration, the Hf hydroxide solution was clouded and a precipitate had formed on the upper surface of the flask. The precipitate was analyzed by IR spectroscopy and was found to contain hydroxide (FTIR, (KBr): n = 3502 cm-1, 1121 cm-1, 961 cm-1). We assume that the precipitate was Hf(OH)4 (s), and not a mixed precipitate. The Hf hydroxide precipitate was visibly different from the Hf carbonate. For comparison, the carbonate had a clear solution with precipitate concentrated in the lowest section of the round bottom flask.
The total hafnium concentration was then determined by ICP-AES. The results are given in Table 3.
Table 3. Hafnium Hydroxide Solubility Data (0.1 M NaClO4 System, 100% Ar)
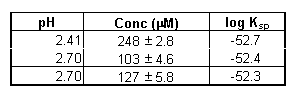
The solubility products listed in Table 3 were then calculated using the stability constants estimated above (Eq. 14). Equation 6 was used to determine the hydroxide concentrations at the given pH levels.
![]()
Solubility and Speciation Calculations
To better understand how effective hafnium would be as a neutron poison for the geological disposal of weapons-grade plutonium, it is necessary to examine how both hafnium and plutonium are expected to behave in the Yucca mountain environment. Using the solubility and stability constants measured for hafnium carbonate and hydroxide, along with some literature values for the solubility and stability constants of plutonium, it is possible to estimate the speciation and solubility limits for both the plutonium and hafnium in solution under conditions similar to those expected at Yucca mountain. For these calculations, the system was modeled as pure water in equilibrium with a partial pressure of carbon dioxide (pCO2) of 10-2.5 atm. [14] with an ionic strength of 0.1 M. Table 4 contains the constants used for these calculations. As the stability constants for the higher carbonato species were not determined in this work, the stability constants for Pu(CO3)32- and Pu(CO3)56- determined by Leirse [6] were used for the stability constants for the Hf(CO3)32- and Hf(CO3)56- in these calculations. The stability constant determined for Hf(CO3)44- by João, et. al. [2] was used for the tetra-carbonato species. The stability constants determined by Leirse were used in these calculations for consistency, as the constants used for the hydroxyl species were also taken from Leirse [6]. The solubility product for Pu(CO3)2 (s) was not necessary as the formation of the plutonium (IV) carbonate precipitate has been found not to be important [15].
Table 4. Equilibrium Constants Used in Speciation and Solubility Calculations
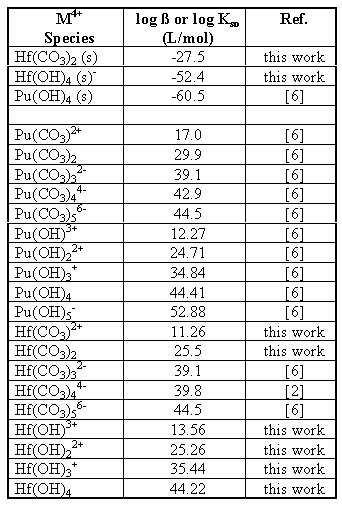
Speciation Calculation
From a mass balance equation for the total metal concentration in solution (Eq. 15a,b) and the definition of the stability constant (Eqs. 8, 4), the relative fraction of free metal present ([M4+]/[M]aq) can be determined as a function of hydroxide and carbonate ion concentrations (Eq. 16). Using this ratio, the relative fraction of each complex can be determined (Eq. 17), where L denotes the ligand (OH- or CO32-). The concentration of the hydroxide ion [OH-] and carbonate ion [CO32-] are determined from the equilibrium relationships given by equations 6 and 5, respectively, for a I = 0.1 M system. By using these equations, it is possible to examine the speciation of the Hf and Pu(IV) without needing to determine the actual free metal ion or total metal concentrations, which means that these estimates can be used for any dissolved metal concentration, provided that the metal concentrations are not high enough that poly-nuclear species become important.
|
|
(15a) |
|
|
(15b) |
|
|
(16) |
|
|
(17) |
Solubility Limit Calculations
Using the same mass balance equations as for the speciation calculation (Eqs. 15-17) along with the definition of the solubility products (Eqs. 7, 11 for Hf, similar equations for plutonium) it is also possible to determine the expected solubility limits for hafnium and plutonium in solution. By assuming that the system is in equilibrium with plutonium hydroxide, Pu(OH)4 (s), the free ion concentration as a function of pH can be determined from the solubility product. From the stability constants (Eqs. 8, 4 with Pu substituted for Hf), the equilibrium concentrations of the various hydroxide and carbonate complexes can be determined, and then used to find the total dissolved metal concentration (Eq. 15a). This value represents the solubility limit for plutonium in equilibrium with the hydroxide solid. The calculation was then repeated for hafnium, assuming that the system is in equilibrium with the hafnium hydroxide solid, Hf(OH)4 (s). Over the pH range examined (pH 3-13), hafnium carbonate, Hf(CO3)2 (s), is always undersaturated for a system in equilibrium with the hydroxide solid. This can be verified by calculating the free hafnium concentration that would be in equilibrium with the carbonate solid (Eq. 7), which will be greater than the free hafnium concentration given by equilibrium with the hydroxide solid for this system over the pH range of interest.
Results
From equations 16 and 17, the relative concentrations of the carbonate and hydroxide solution species for hafnium and plutonium were calculated for the simulated Yucca Mountain system (pCO2 = 10-2.5 atm., I = 0.1 M). The results of these calculations are shown in Figures 1 and 2 as a function of pH. To simplify the plots, only the species that account for more than 25% of the total solution concentration at any pH are included below.
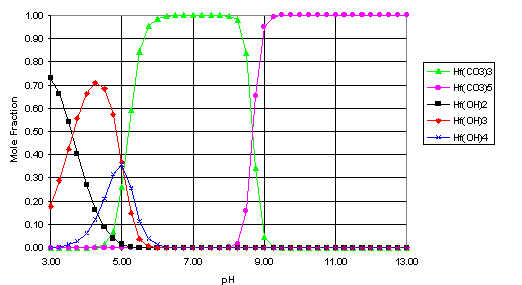
Fig. 1. Speciation of Hf (I=0.1 M, pCO2=10-2.5 atm.)
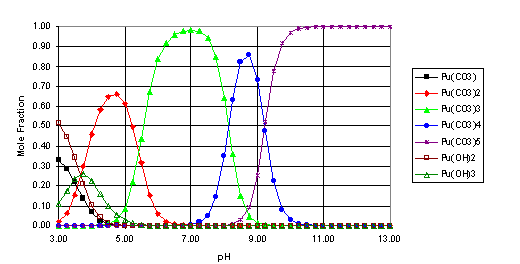
Fig. 2. Speciation of Pu(IV) (I=0.1 M, pCO2=10-2.5 atm.)
The solubility limits for a system in equilibrium with the metal hydroxide solids (Pu(OH)4 (s) and Hf(OH)4 (s)) was calculated using equations 15a, 16, and 17. The free metal ion concentration was given by the solubility product (Eqs. 7, 11), and the ligand concentrations were determined using equations 5 and 6. The log of the solubility limits for hafnium and plutonium are shown in Figure 3 as a function of pH.
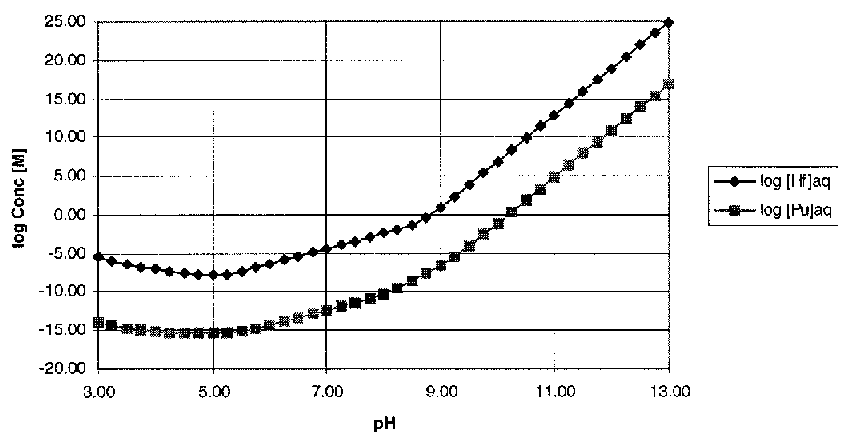
Fig. 3. Solubility Limits for Hf and Pu(IV) (I=0.1 M, pCO2=10-2.5 atm.)
CONCLUSIONS
From the hafnium carbonate solubility data it was possible to determine the solubility product (Table 4) as well as the stability constants for the first 2 hafnium carbonate complexes (Table 4). These results are similar to the stability constants observed for plutonium (IV) carbonate in the literature (Table 1). From the hafnium hydroxide titration, it was possible to also estimate the hydrolysis constants and the hafnium hydroxide solubility(Table 4).
From the solubility calculations (Figure 3), it appears that the hafnium will be significantly more soluble than the plutonium (from 5 to 7 orders of magnitude more soluble depending on pH). This suggests that if the release rate from the WGPu host form of the hafnium and plutonium (IV) is controlled by solubility of the hydroxide phases, the hafnium will be depleted from the host form before the plutonium. Also, the curve suggests that it may be possible for plutonium to be precipitated out of solution in situations where the hafnium is still soluble. The dominant reason for the difference between the Hf and Pu(IV) solubility curves is the difference in the solubility products.
From the speciation calculations (Figures 1 and 2), it seems that, over much of the pH range examined, the solution species of Hf and Pu(IV) will be dominated by the carbonate complexes, particularly the M(CO3)32-, M(CO3)44-, and M(CO3)56- species. The strength of these complexes is also a significant factor in the solubility of both metals at high pH. As these complexes seem to have a significant impact on the behavior of hafnium and plutonium (IV) in this simulated Yucca Mountain environment, it would seem that more effort is needed to determine these stability constants more accurately (for example, the literature values for the stability constant for Pu(CO3)56- listed in Table 1 range over 30 orders of magnitude). Also, this work focused only on the Pu(IV) oxidation state. In an oxidizing environment, such as Yucca Mountain, the plutonium may be oxidized to the Pu(V) state[16], which would significantly alter its speciation and transport behavior and would change the effectiveness of Hf as a potential neutron poison for the disposition of WGPu in the geological repository.
Future work should attempt to determine the stability constants for the higher hafnium carbonate complexes. The goal should ultimately be to use these constants, along with existing geochemical models (such as EQ 3/6) to examine the behavior of hafnium and plutonium in the Yucca Mountain repository environment. Criticality assessments could then be performed with the SCALE-PC code to examine the effectiveness of the hafnium as a neutron poison as compared with other neutron poisons examined previously [10].
ACKNOWLEDGEMENTS
This work is supported by Lawrence Livermore National Laboratory subcontract number B338670, ADetermining Complexation Parameters for Hafnium, Lanthanides, and Plutonium@.
REFERENCES