EDF CONCRETE WASTE PACKAGES & DISPOSAL SAFETY -
PREDICTION OF RETENTION OF RADIONUCLIDES
EVEN IN CASE OF CRACKS
Bernard PONCET
EDF - Electricité de France
D.E.P.T. Immeuble Cap-Ampère
B03.092, 1 place Pleyel
93207 Saint Denis Cedex 1, France
Bruno GERARD
EDF - Electricité de France
Research and Development Division, Centre des Renardières
77818 Moret sur Loing cedex, France
ABSTRACT
Different concrete waste packages have been designed by Electricité de France (EDF) for the long-term storage of Low Level and Intermediate Level radioactive Waste (LLW & ILW). Their main function is to confine radionuclides from biosphere for three hundred years in a near-surface disposal.
According to the disposal regulation, a concrete container is needed for few waste like high activity water filters. The water filters from EDF nuclear power plants are encapsulated in mortar which is poured into the concrete container. French reference scenario of concrete degradation during near-surface disposal considers a degradation distribution law and an original method is presented to quantify the influence of cracks on the retention.
First, the different chemical and physical processes involved in the containment of radionuclides are analysed. Secondly, the effect of the presence of a network of cracks on the mortar and concrete retention are discussed. Thirly, in order to prove the performance of the confinment even in case of cracks, a simplified model is proposed to predict the radionuclides release with time.
It is concluded that cement-based materials offer high performances as mechanical and chemical barrier to the radionuclides releases for concrete container in a near-surface disposal.
PACKAGES - TECHNICAL DESCRIPTION
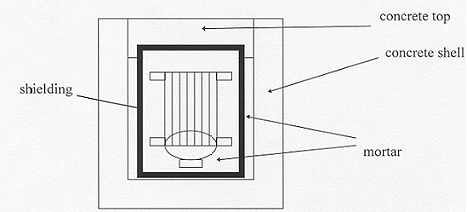
Figure 1 shows a schema of an EDF water filters package. The waste is put in a precast concrete container reinforced with steel near the cap. Steel reinforcement is designed for engineering considerations : minimal reinforcement for limiting cracking due to bulk shrinkage during hydratation, and additional reinforcement for the transportation drop tests. The cap area appears to be more brittle than the bottom area, so the additional steel reinforcement is concentrated in this zone. A new generation of concrete is used for precast containers, characterized by a compressive strength of 84 MPa at 28 days and a water permeability lower than 10-13 m/s. These performances result from the addition of silica fume and superplasticizers to the mixture.

Figure 1 - Simplified design of a package for a water filter
A steel liner and a synthetic thermal insulator are used as lost formwork during container casting. The thermal insulator minimizes strain development during container filling and cement hydratation. A layer of lead or iron can also be added, especially for high activity water filters, for shielding purpose. Finally, the water filters are placed in the container and blocked by a mortar. This mortar is directly in contact with radionuclides.
The aim of this paper is to detail the efficiency of the cementitious materials for radionuclide retention in the shallow disposal "Centre de Stockage de l'Aube" (ANDRA).
CEMENT-BASED MATERIALS : A BRIEF REVIEW
This section focuses on a breief rewiew of the fundamental physical properties of cement-based materials. Clinker is obtained by heating limestone (80%) and clay (20%) up to about 1450°C. After beeing ground to a high specific surface area (200-500 m2/kg), the resulting powder consists of three mineralogical phases : calcium silicates (3CaO.SiO2, 2CaO.SiO2), aluminate (3CaO.Al2O3) and aluminoferrite (4CaO.Al2O3.Fe2O3) [1]. Gypsum (CaSO4.2H2O) is added to the clinker (~5% of clinker weight) in order to control the setting kinetics. Then, the resulting product is an Ordinary Portland Cement (OPC). Mechanical and chemical strengths are initiated by mixing OPC with water. Complex chemical reactions accur to form solid hydrates. This change from a liquid to a solid state is accompanied by heat generation and shrinkage. These hydrates consist of three main new mineralogical phases : portlandite (Ca(OH)2), hydrated calcium silicates (xCaO.SiO2.nH2O), calcium aluminate systems (ettringite, monosulfate, etc.). About 60% of the total mass are made of hydrated calcium silicates also called C-S-H. More water than needed for total hydratation of cement particles is used when mixing water with OPC. The excess of water is responsible for the creation of a porosity which can vary between 8% and 60% for an OPC paste. The lower the water cement ratio (w/c), the lower the porosity.
Pore sizes which constitute the porosity vary from 20.10-10 m to about 20.10-6 m. Assuming pores as small cylinders, the average pore radius is about 3 to 5. 10-8 m. Then, it must be noticed that whereas the pore sizes are quite small, the resulting pore surface area is very large. This is a major characteristic of cement-based materials.
The addition aggregates with sizes < 5 mm leads to a mortar. For aggregate sizes > 5 mm, the mixture becomes a concrete. The compressive strength of a cement-based marerial varies from about 20 MPa up to about 150 MPa or even more if thermal and (or) mechanical treatments are performed [2]. This range of values depends on w/c, the use of superplasticizer and additives (silica fume, filler, etc.). Then, cement-based materials offer a very competitive material to design mechanical barriers. Moreover, thes chemical materials can also be regarded as a very good chemical barrier for toxic elements as discussed now.
At the molecular scale, several authors have shown that C-S-H could be represented as the superposition of SiO2 layers an Ca layers (Figure 2). OH- and H2O form the links between these layers, which brings the structural stability of C-S-H crystals. The layer length is known to depend on the Ca/Si ratio. The lower Ca/Si, the longer the SiO2 layers. This rati varies between 1.7 (pH>12) and 0.5 (pH<8). These molecules have the property to fix other chemical elements as Cobalt, Americium, Plutonium, etc. This phenomenon is obtained either by chemical retention (substitution- or insertion - of atoms), or by physical retention (surface adsorption). This property of retention is also valid for other hydrates : chemical retention of 14C is obtained with portlandite - Ca(OH)2 - to form carbonates : chlorides are mainly retained by aluminates, etc. A retention parameter (Kd) can be experimentally determined as a function of the chemical element and the material :
|
|
(1) |
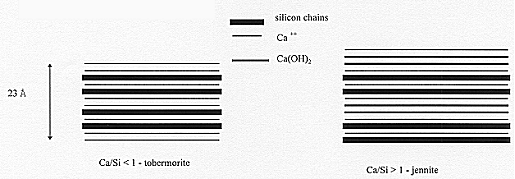
Figure 2. Structure of C-S-H from [5]
The concentrations are understood in the total volume and the sum of free and bound concentrations give the total concentration of the element. This definition of Kd (no dimension) is usually expressed in m3/kg (volume of pore solution/mass of solids). A simple relation exists beetween Kd defined in eq. (1) and the parmeter published in m3/kg, called Kd* in this paper :
|
|
(2) |
Table I shows values of Kd* for several radionuclides in a cementitious material [3]. Assuming a density of 2000 kg/m3 and a porosity of 0.2, a value of Kd is also calculated. It must be noticed that Kd values vary in the range of 10-5.104. That means that the majority of radionuclides are fixed in the solid. A very small quantity is free to migrate in the porous network and finally to the environnement.
Table I. Experimental data for Kd*- density = 2000 kg/m3 and porosity = 0.2
|
Species |
Kd* |
|
C |
5 |
|
Ni |
1 |
|
Tc |
0.001 |
|
Nb |
1 |
|
Pu |
5 |
|
Am |
5 |
|
Pd, Sn |
0.2 |
|
Zr |
1 |
|
Cs, Sr |
0.002 |
|
I |
0.03 |
|
Th |
5 |
|
U, Np |
5 |
The main difficulty when modelling is to find representative experimental data, given that the interaction (retention) between solids and radionuclides strongly depends on the pH and on the ionic strength of the pore solution. That is why a sensitivity analysis must always be done when a performance assessment is achieved.
MODELLING MIGRATION IN A SOUND POROUS MATERIAL
When placing fresh mortar around filters, radionuclides are leached from the filter to the fresh mixture. Then the only mechanism that occurs is the migration of radionuclides in the mortar through the porosity. The driving force is a difference of concentration beetween the filter area (active zone) and the environment (no presence of radionuclides). This phenomenon is called diffusion. The diffusion speed at each point of the container is defined by the following equation :
|
|
(3) |
where D is the coefficient of diffusion in m2/s, Cf is the free concentration of the considered radionuclide, related to the volume of the material (not only to the volume of the pore solution). The kinetics of diffusion is given by the mass conservation equation :
|
|
(4) |
D
is the Laplacian operator. With C=Cb+Cf and eq. (1), eq. (4) becomes :|
|
(5) |
where Dapp is the apparent coefficient of diffusion. The higher Kd, the slower the kinetics of radionuclide release. Given that radioactivity can be associated with a loss of mass for some radionuclides, the concentration is modified as follows :
|
|
(6) |
where M represents the coordinates of a given point, T is the radioactive period. Assuming a 1D diffusion process, eq. (5) becomes :
|
|
(7) |
M0 represents the coordinates of the surface of the filter and L is the thickness of the mortar barrier. The boundary conditions are :
|
|
(8) |
with :
|
|
(9) |
The total release in the environment of a specific radionuclide can be determined as follows :
|
|
(10) |
Considering an initial spectra of radionuclides and values of retention given in Table I, it is concluded that the release of radionuclides after 1 year from a sound material (uncracked) is very low.
Moreover, the loss of mass related to the radioactivity only concerns a emitters such as actinides, whose period T is very long. So the contribution of their radioactive decrease to the evolution of their concentration is very low compared to the influence diffusion. As for b -g emitters, whose period is shorter, their radioactive decrease has intrinsically no influence on their concentration. Hence, we will from now on neglect the contribution of radioactivity to radionuclides transport.
RETENTION AND RELEASE IN CRACKED POROUS MATERIALS
In the shallow disposal, we can assume the presence of cracks in cement-based materials as the manifestation of its limited durability. Let us propose the following pessimistic and simplified approach to model the consequences of the presence of a network of cracks on the release of radionuclides. Figure 3 shows the physical model used for the demonstration. Craks are modelled by parallel planes with a regular interval « d » with an average effective crack width « w ». Cracks are assumed to be saturated by water for diffusion. This is a very pessimistic hypothesis. indeed, for an average relative humidity of 75%, it should be noticed that cracks would dry and transport of radionuclides by diffusion would be impossible.
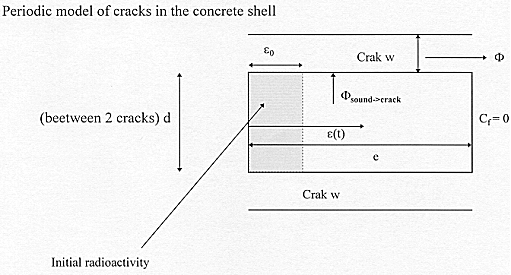
Figure 3 - 1D Crack model and parameters
The "black-box" approach :
Eq. (5) gives the kinetics of diffusion in the sound part of the material (between cracks). The effective diffusion coefficient in cracks is equal to free diffusion of water :
Dcracks=10-9 m2/s.
Leaching of radionuclides occurs owing to this difference of diffusion kinetics between cracks and sound medium and due to the Dirichelet boundary condition at the external surface : Cf=0.
Then, a flow F1 which quantifies the release from the sound material and flow F2 which stands for the release from cracks can be calculated as a function of the geometric parameters and the initial distribution of radionuclides obtained by solving equations (5) to (9.b). The total flow of radionuclide is then :
|
|
(11) |
This problem can be easily solved by finite analysis for example. Here, we propose to introduce a simplified analytical approch to estimate and quantify the release of radionuclide as a function of various parameters (thickness, cracks, marerial properties). The major interest of it is to provide us more explanations about the physical phenomenon.
A simplified analytical approch :
First, this approch is developped for one radionuclide, its generalisation to a population is secondly introduced. Let us consider e0, the depth reached by the radionuclide during the setting of the cement paste. e(t) is the maximum depth reached by the radionuclide until a time « t » (by simple diffusion through the sound material).
Assuming a semi-infinite medium, and that e (t) is actually evaluated as the limit of a volume containing 95% of the initial radionuclide activity, we obtain :
|
|
(12) |
In order to evaluate the flow across the external surface with no contribution of cracks, a conservative way consists in assuming that effective thickness for radionuclide diffusion becomes : e-e (t) (see Fig. 3), with a constant activity between the internal medium and e (t) (equal to the average activity in this volume). This hypothesis is of course an overvaluation of the actual distribution of the radionuclide. Then, the release fraction (RF) after cracking occuring at date « t », which is the ratio between the activity released after time « t » and the total activity at this time « t », is obtained by integrating the release of radioactivity across the external surface during a period « D t » [the initial activity is equal to 1, so the average activity up to e (t) is equal to 1/e (t), and the diffusion length is (e-e (t))] :
|
|
(13) |
Let us now evaluate the release considering the leaching of radionuclide through cracks and their diffusion in cracks (F sound->cracks in Fig. 3). For infinite values of « w » the crack area must be considered as an external surface. Then the RF value is obtained by modelling a block of porous material saturated with an homogenized activity, of lengh e (t)/3 and thickness « d » plunged into pure water. For large « w », a problem of pure leaching with Dirichlet boundary conditions at the crack surface (Cf=0) is solved and RF becomes :
|
|
(14) |
For values of « w » occuring with the time in the disposal, the leaching from sound material to the environment is not instantaneous. A delay due to diffision process in the porous medium and in cracks occurs. The lower the crack width, the longer the delay. It must also be noticed that the thicker the material (« e »), the longer the delay. The delay of migration in the crack is added to eq. (14) by virtually increasing the distance betveen two cracks of a 2 « x » value.
The mean length is starting from :
|
|
(15) |
So, the flow F 2 (see Fig. 3) can be written :
|
|
(16) |
Thus, x can be evaluated considering that there is no interaction on this length (Kd=0) :
|
|
(17) |
where « p » is the porosity. Then, the equality between eq. (16) and (17) must be verified. x is determined :
|
|
(18) |
Eq. (14) becomes :
|
|
(19) |
By summing the contribution of the sound material (eq. 13) and the influence of cracks (eq. 19), we have :
|
|
(20) |
We can see the influence of the barrier thickness « e » on the radionuclide release. It is noticed that due to good retention properties and low diffusivity, the release fraction value remain low even in the presence of cracks.
CONCLUSIONS
Numerous data show the efficiency of cement-based materials to retain radionuclides. These materials are well adapted for the confinement of radioactive species. In this paper, a new approch has been introduced to evaluate the radionuclide release tthrough porous materials considering diffusion and interactions phenomena. The major contribution concerns the influence of cracking on retention properties of cement-based materials. A simplified analytical model is proposed taking into account material properties as well as cracking parameters. It is noticed that crack width is a main parameter. Nevertheless, it is shown that the release remains low in the presence of crack, this is due to high retention properties and low diffusivity of these materials. For performance assessment, it is also shown that the main parameter are the diffusivity and the retention coefficient Kd.
REFERENCES
|
[1] |
F.P. Glasser and M. Atkins "Cement in Radioactive Waste Disposal"
|
|
[2] |
P. Richard - "Reactive Powder Concrete : a new ultra high strength cementitious material"
|
|
[3] |
J. Crank - "The mathematics of diffusion"
|
|
[4] |
B. Allard - "Radionuclide sorption on concrete"
|
|
[5] |
H.F.W. Taylor - "Cement Chemistry"
|