A CRITICALITY ASSESSMENT OF VITRIFIED WEAPONS -
GRADE PLUTONIUM IN GEOLOGIC STORAGE
K. Budlong Sylvester and S. A. Simonson
Massachusetts Institute of Technology
NW12-307, 138 Albany St.
Cambridge, MA 02139
ABSTRACT
A coupled glass dissolution and criticality model was developed to assess the potential for a repository criticality event resulting from plutonium disposal. Bounding calculations indicated that the reference waste glass could reach a critical state due to glass reaction with groundwater, and subsequent boron removal, at weapons-grade PuO2 loadings greater than 0.45 wt%. The addition of relatively small quantities of rare earth elements (Gd, Sm, Eu) were shown to increase the predicted time to criticality from thousands to millions of years, however indefinite subcriticality could not be guaranteed under the range of assumed environmental conditions.
INTRODUCTION
In its January, 1997 Record of Decision the US Department of Energy decided to immobilize at least 8 MT of surplus weapons-grade plutonium. Vitrification is currently under evaluation as an immobilization alternative. While processing schedule and cost issues provide incentives to maximize the Pu concentration in glass, criticality concerns during geologic storage may limit Pu loading.
Over extended periods of exposure to groundwater, sufficient neutron absorbers could migrate from the near field to induce criticality. Plutonium has a half-life of 24,000 yrs and decays to fissile U-235 which has a half-life of 704 million years. Both elements can be relatively insoluble. Criticality is a concern as fresh fission products would be given an aqueous transport pathway, potentially to the biosphere.
In order to perform a near-field criticality assessment it was necessary to understand and model the physical mechanisms and spatial changes of an environmentally altered waste form. A model of this behavior was constructed and used to produce "snapshots" of system configuration during the reaction progress. Available data on glass/groundwater chemistry were used to determine reacted glass and solution composition over time. This information was used to calculate the effective multiplication factor (keff) of the system as a function of time. System parameters were then varied to determine their effect on subsequent criticality calculations. In this way parameters of potential importance can be identified for future investigation.
A GLASS REACTION MODEL
The following physical situation was modeled. The model assumes a single glass log with the dimensions of a Defense Waste Processing Facility (DWPF) log (3 m long x 60 cm diameter) and a nominal plutonium loading. The composition of the glass was assumed to be a borosilicate glass used at the DWPF. This would represent the alternative of vitrifying Pu directly with HLW.a
The log was assumed to be placed in a horizontal drift at a repository with conditions similar to those expected to be found at Yucca Mountain in the state of Nevada. The mountain is under investigation as a potential high-level waste repository. A particular geologic formation known as "tuff" was taken to be the reference composition of the host rock.
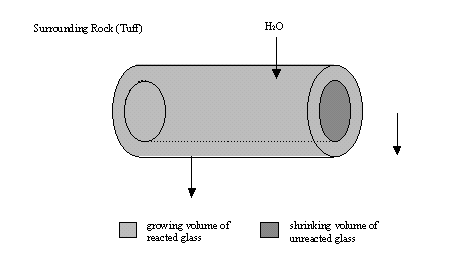
As water infiltrates the emplacement it reacts with glass, producing an annular region of alteration layers (to be described below). This layer moves into the glass as the reaction proceeds. The depletion of soluble poisons in this region may lead to a criticality event. Figure 1 is a graphical representation of the system as it evolves.

Figure 1. Horizontal drift emplacement
Glass Reaction with Groundwater
Glass reaction is a complex process dependent on both glass and solution properties. In general, glass will react with water to release its soluble species and form more stable amorphous and crystalline phases. It is the redistribution of neutronically relevant nuclides during this process that was of primary interest in the work presented here.
Extensive research has been performed on glass reaction with water, the results of which have led to various descriptions of the glass dissolution process. One theory is that H+ diffuses into the glass matrix and undergoes ion exchange, typically with alkali metals such as sodium (prevalently at the non-bridging oxygen sites). The alteration of the glass also allows soluble species (such as boron) to enter into solution. This produces a reacted layer that retains the amorphous silica structure of glass but with concentration gradients of alkali and soluble species. This layer has been termed the "diffusion layer."
Over time, the most depleted portion of the diffusion layer (its outer fringe) begins to hydrolyze. This results in a restructuring or repolymerization of the Si matrix into a more stable, hydrous "gel layer." The process apparently excludes metals incapable of entering into a new amorphous phase [1]. Eventually, the gel layer further reacts with water and is dissolved completely, releasing silica into solution. This reaction is termed "network dissolution."
This surface layer (the diffusion layer and gel layer combined) is typically less than a micron in thickness and moves into the glass as the bulk reaction proceeds. Following behind it is a layered region of amorphous and crystalline phases termed alteration layers. This region has a complex elemental composition. Many of the metals that were either "kicked out" during gel layer formation or released as a result of network dissolution, quickly precipitate to form the alteration layers. These layers can be either amorphous or crystalline in nature. The retention of fissile nuclides (and control elements) in these layers is of interest here.
Kinetics
It is the general consensus that the bulk dissolution rate of glass is primarily controlled by silica concentration in the leachate [2]. As the glass reaction proceeds, Si species build up in solution and the Gibbs free energy of the system approaches its minimum (equilibrium) value. This "saturation" effect slows glass reaction rates.
The adoption of such an affinity model suggests an important role for the alteration layers. The alteration layers may control the concentration of the rate-limiting species in solution. This may explain why in closed system leach tests saturation is not reached. A "residual affinity" is observed that keeps the glass reacting. It may be the case that the formation of the alteration layers and/or the nucleation and precipitation of a particular phase reduces solution concentration and maintains the residual affinity. In this case, as long as the phase can precipitate, the solution will never reach saturation with respect to the alteration layer. Predicting the formation of the rate controlling phase(s) is a major challenge in long-term glass reaction modeling.
Model Assumptions
In the model, Pu loaded glass is exposed to groundwater. As the glass reacts, its components enter into solution. The aqueous species react and insoluble phases are formed which make up the alteration layer. The concentration gradients in the surface layer were assumed insignificant. The composition of the alteration phases was assumed to be those predicted using the speciation/solubility code EQ3/6.
The alteration layer is produced at an average bulk dissolution rate (BDR). The BDR was not calculated using an affinity model. As noted previously, the long-term reaction rate may be controlled by an unknown silica phase. Rather than assuming control by various phases, the BDR was taken as an exogenous input and varied to gauge its effect.
Fixing the BDR at a constant value determines the radius of the unreacted radius as a function of time. With a constant BDR (and assuming dissolution occurs only in the radial direction) the radius of the log goes as:
![]()
where Rlog(t) is the radius of the unreacted log at time t, Ro the initial radius and r log the density of the glass.
As reaction equilibrium is assumed, the predicted phases determine the concentration of glass elements in solution. This concentration combined with the infiltration rate of water in the repository determines the removal rate of elements from the layer.
Using these assumptions a set of mass balance equations for elements in the alteration layer was developed. The radius of the unreacted log fixes the rate at which elements are added to the alteration layer, while decay and volumetric flow set the removal rate. Knowing the production rate and removal rate of elements in the layer, the following rate equation was constructed:
![]()
where Ni is the mass of nuclide i in the alteration layer at time t, fi(t) its mass fraction in the log, Csol its solubility limit and l i its decay constant. The length of the log is fixed by L and I is the water infiltration rate in the repository. The effective cross-sectional area (A) is needed to determine the volumetric flow rate through the emplacement. An "interaction" thickness of 5 cm was added to the initial radius of the log for calculating this area. As the radius shrinks, a larger portion of water will "miss" the unreacted glass as it represents a smaller target. However, it is assumed that the initial "effective" borehole will provide a constant reaction volume for the glass/water mixture. This is conservative as a smaller volume of water would reduce neutron control removal rates. In addition, we are interested in removal of elements in the entire reacted region, not just the layers near the log.
This general equation can be written for each glass component. For U-235, an additional buildup term due to the decay of Pu-239 is needed. The resulting set of equations can be solved using the elemental composition of fabricated glass as the initial condition to give a relationship for the mass of each nuclide in the alteration layer over time. The differential equations were solved numerically using a Runge-Kutta method.
The bulk dissolution rate, water infiltration rate and elemental loading can be varied to determine their effect on criticality. The remaining information needed is the solubility data. The following section describes how this information was attained.
SOLUBILITY/PHASE CALCULATION
Whether glass elements remain in solution or precipitate is determined by the contacting groundwater conditions. Over time, the glass reaction itself will alter solution chemistry. Available thermodynamic data were used to investigate the evolution of solution concentrations during glass reaction and the formation of precipitate phases. (Sorption or colloid formation may also occur but was not modeled here.) The composition of the phases over time was used to determine if the near field system approaches a critical condition.
The behavior of the following elements was examined: Pu, U, B, Li and Eu. Plutonium and uranium are fissile elements. While little uranium is found initially in the glass, Pu-239 decays to produce fissile U-235 (Pu-239 half-life=24,100 yrs). Boron and lithium are neutron control elements that are normal components of the glass. It is the higher solubility of boron and lithium relative to Pu and uranium in solution that could lead to a criticality event.
Europium is a neutron absorber not used in the current DWPF glass frit that was evaluated for its neutronic control capabilities and its expected insolubility. Europium was identified in prior work by the author as being particularly detrimental to a Pu explosive device if not removed [3].
The oxidation state and the degree of complexation will depend on solution composition. As the assumed repository is Yucca Mountain, water from a well located at the site (J13) was taken as the reference solution. The J13 water is neutral pH and slightly oxidizing. It is a carbonate water with significant amounts of silica, sodium and calcium. Notably it also contains sulfate and fluoride species which are known to form complexes with actinides.
The speciation/solubility code EQ3/6 was used with its associated thermodynamic databases to determine solution concentrations as the glass reacts [4].b EQ3 uses mass action and redox relationships to solve for the thermodynamic equilibrium state of a specified ground water, identifying species concentrations and supersaturated phases. The order of phase precipitation, which may allow initially supersaturated species to remain in solution, is not addressed.
EQ6 models the addition of reactants to a solution allowing supersaturated phases to precipitate as reaction proceeds. The order of precipitation is determined by the degree of disequilibrium of the saturated phases. After the phases are removed, additional reactants are added and the process repeats. The onset of saturation can be observed in this way.
EQ6 was run in titration mode to model the effect of dissolving glass. In the titration calculation glass components are stoichiometrically added to a constant volume of water where they are completely dissolved and new phases are allowed to precipitate. The calculation results in a description of the aqueous species and insoluble phases that form during reaction progress. Points along this reaction pathway were taken to represent alteration layer composition for various degrees of glass reaction. The associated phases and solution concentrations were then used in the analysis.
Solubility Results
Elemental solubilities used in the dissolution model were calculated based on equilibrium with phases formed during various stages of glass reaction. The elements of 10 grams of DWPF glass were added stoichiometrically via a titration process into one kilogram of J13 water. The glass contained 8 wt% PuO2 and one mole of Eu2O3 per mole of Pu.
EQ6 produced a history of phase production and solution chemistry during glass reaction. Figure 2 shows how the concentration of the relevant elements changed over time. At no time during the reaction were Li or B predicted in the alteration layers. (Boron and lithium concentrations are initially constant as both are present in the contacting J13 water.)
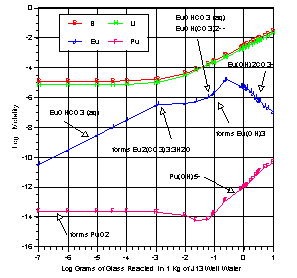
Figure 2. Reaction Path for DWPF Sludge-Supernate Borosilicate Glass in J13 Well
Water from Yucca Mountain
Europium enters into solution as the carbonate species EuOHCO3 and eventually precipitates as Eu2(CO3)3:3H2O. When HCO3- starts to drop, Eu(OH)3 begins to form. Competition ensues between the formation of several carbonate complexes and precipitation. Ultimately Eu reaches a maximum concentration of 1.5E-5 M. Europium concentration is then reduced with increasing pH caused by the glass reaction itself. Europium remains in the +3 state throughout glass reaction.
Plutonium from the glass is immediately precipitated as PuO2 (log Ksp=-7.36). The small amount remaining in solution exists in the +5 and +6 state (PuO2+ and PuO2F3-). As glass reaction continues, Pu concentration dips due to HCO3- reduction to a concentration of 5.8E-15 M. Eventually Pu hydrolyzes (complexes with OH-) causing the solubility of Pu to increase. This complexation allows the Pu to be more soluble under reducing conditions than earlier oxidizing conditions. Pu solubility is then controlled by pH.
Replacing the Pu with equal molar U in glass provided similar information. As the glass reacts, the uranium concentration rises until haiweeite forms (Ca(UO2)2 (Si2O5)3:5H2O). The carbonate complex UO2(CO3)34- keeps the U concentration initially at approximately 1E-9 M, otherwise the concentration would have been much lower. As pH drops and HCO3- concentration is reduced, uranium concentration drops to a minimum value of 2.6E-10 M. As the glass continues to react, uranium in the +4 state forms aqueous U(OH)4, causing uranium concentration to rise. Eventually no carbonate complexes exist and uranium is in equilibrium with uraninite. Uranium concentration stabilizes as solution pH stabilizes. For determining U solubility, the initial U loading was not important.
Carbonate and hydroxide appear to be the most significant complexing agents in the system studied. While chloride and nitrates are present in J13 water, at no time do Pu or U form their complexes. This is consistent with the observed trend in complexation strength. It is the "over" complexation of the actinides (hydroxide and carbonate) to produce negatively charged species that could increase solubility in the J13 water.
The oxidation potential appears to be sensitive to the combined Eu and Pu loading. Without these elements the eH drops roughly 0.2 mV during glass reaction. With these elements it drops 1.2 mV. This reflects the strong reducing properties of rare earths and actinides. In contrast the loading of these elements does not affect pH.
The worst regime from a criticality perspective appears to occur when pH is around 9. This produces the greatest difference between Eu and Pu solubility. Uranium concentration is relatively constant throughout glass reaction. At higher pH Eu becomes less soluble, reducing this difference and the criticality concern. Due to the ion exchange reactions of dissolving glass, the groundwater closest to the surface is likely to be basic.
KEFF CALCULATION
For the criticality assessment the lowest solubility achieved by the fissile elements was used with the highest calculated solubility for the control element. This was done to represent a conservative estimate of the highest potential for fissile/control separation. This information was combined with various estimations of bulk dissolution rate and water infiltration rate to examine the potential for criticality to occur in the near-field.
The system was modeled as three regions: the unreacted glass, the alteration layer, and the surrounding tuff. The unreacted glass was assumed to be comprised of the major components (>1 wt %) of the glass. Various amounts of Pu and rare earth elements (REE) were added to this composition. The neglected components could contain neutron absorbers so their exclusion was deemed conservative.
The porosity of the tuff was taken to be 0.3. While unfractured tuff is likely to posses a lower porosity, the tuff backfill would not due to disruption during emplacement. This value provided a upper bound on the amount of water that could be found in the tuff. After determining the concentration of the relevant nuclides in the alteration layers the remaining mass of alteration layer was assumed to be amorphous SiO2. The total mass of the alteration layer was assumed to be 25% of the original glass. This also fixed the porosity of the alteration layers at 0.75.
After fully characterizing the system, the compositional information was used to determine the system keff over time using the criticality code system SCALE-PC. SCALE-PC is a modular code system for performing criticality safety analysis [5]. It is comprised of various functional modules for cross section processing, criticality and shielding calculations. The XSDRN-PM module was used to produce 1-D, discrete ordinates, solutions to the neutron transport equation.
A repository containing dissolving glass logs was modeled as a lattice of infinitely long, annular "fuel" cells. However, the pitch was chosen large enough so that neighboring logs would not contribute to the neutron economy. The alteration layer, depleted of boron, was modeled as the fuel region of a large annular fuel pin. The interior region contained the unreacted glass and the tuff represented the moderator portion of the unit cell.
Results under "Worst Case" Conditions
In the interest of bounding the criticality problem a set of criticality calculations were performed using values most favorable for control removal and fissile element precipitation. The model parameters bulk dissolution rate and volumetric flow were set their highest values, 0.1 g/m2/d and 0.01 m3/m2/yr. These assumptions were assumed to represent a "worst case" scenario.
Initially, a glass loaded with 8 wt% PuO2 was modeled. Without additional Eu, the model log was shown to go critical well before it was completely reacted. Figure 3 shows the results for the 8% PuO2 case with no Eu under the "worst case" conditions of extremely low durability and high water infiltration rate. The boron in the unreacted glass did not provide significant criticality control. The hydrous alteration layer loaded with fissile elements was too reactive. It appears that the relevance of boron in the glass is low for criticality control purposes and additional control is needed.
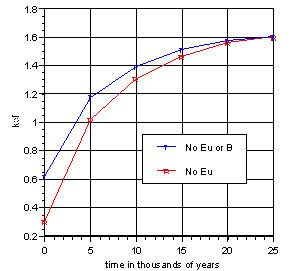
Figure 3. Boron Control (8 wt% PuO2)
Figure 4 shows the effect of control element removal for a glass log loaded with 8 wt% PuO2. Even at the assumed maximum Pu loading, only a relatively small concentration of Eu is needed to hold down reactivity. Both the thermal neutron cross section and resonance integral of Eu-151 are an order of magnitude higher than those of Pu-239. A mole ratio of 1/2 Eu to Pu kept the system subcritical for more than 800 thousand years. Due to the atomic mass differences between Pu and Eu, this corresponded to a loading of less than 3 wt% Eu2O3 (2.6 wt% Eu).
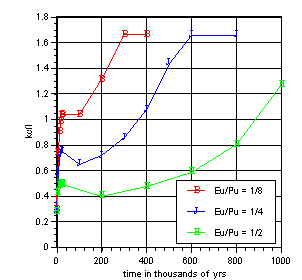
Figure 4. Europium Loading Effect (8 wt% PuO2)
As the Figure shows, while Eu was able to control criticality for hundreds of thousands of years, the critical state was ultimately reached. Europium eventually exited the near field entirely while sufficient U-235 remained. The system required only 0.014 g/cc U-235 to be present in the alteration layer to go critical. After 1 million years the U-235 concentration was 0.18 g/cc. Uranium's insolubility and 704 million year half-life assured that it would remain over the time period examined.
In the model, Eu loading was an effective method for extending the time to criticality. However, if criticality at any time is viewed as unacceptable, this strategy may not be sufficient. If an absolute loading limit of 30 wt% Eu is assumed (i.e. a waste glass loaded only with Eu), for the worst case conditions, Eu will be gone after 13 M years. The concentration of U-235 will remain well above 0.014 g/cc at this time. If subcriticality must be assured over this time period, relying solely on dissolved Eu in the glass may not be sufficient.
The physical mechanisms affecting keff can be elucidated by a close examination of Pu/ Eu/U system behavior over time. Initial glass dissolution and removal of soluble poison increased the neutron multiplication of the system. After 23,000 years the entire glass had reacted and keff began to drop as Pu-239 decayed to U-235. However, this reduction was countered by the removal of Eu. Eventually, Pu-239 completed decayed and additional Eu losses caused keff to rise to its limiting level, slightly above 1.6.
Reduced plutonium loading can limit the keff of the system. Reducing the Pu concentration from 8 to 2 wt% pushed the time to criticality to roughly 225 thousand years. However, increasing the Eu concentration from 0.65 to 2.6 wt% pushed the time to criticality to approximately 900 thousand years. While Pu loading was effective at limiting the maximum reactivity possible, it was the Eu concentration that had the larger impact on when criticality occurred.
Nonetheless, the potential for diluting Pu to a level below which criticality cannot occur under the worst case conditions would be possible. It was determined that a loading of 0.45 wt% PuO2 would keep the initial peak in keff below 1.0 without added reactivity control.c The benefits of this approach would have to be weighed against the increase in disposal costs as more than 6600 additional DWPF size canisters would be produced. This is more than the 6105 canisters of vitrified HLW waste the DWPF facility is already scheduled to produce over 20 years of operation [6].
The presence of a moderator was shown to have a significant impact on criticality. Calculation showed the system to be undermoderated at all times. The spectrum benefits of added water outweighed the additional hydrogen absorption. Full saturation of the 0.75 porosity alteration layer was not required for the system to go critical. Less than 25% saturation was needed for a glass loaded with 8 wt% PuO2 and an Eu/Pu mole ratio of 1/8.
The effect of reducing the bulk dissolution rate was also evaluated. This corresponded to scenarios of improved glass performance. The better performing glass effectively eliminated the local keff maximum observed during the early stages of less durable glasses discussed above. The effect of Pu-239 decay to U-235 was also masked by the longer-lived glass. However, even glasses possessing the best expected long-term durability (BDR=0.001 g/cm2/yr) cannot guarantee subcriticality indefinitely. The slowly growing alteration layer is completely depleted of Eu and a critical condition is reached.
Reducing the volumetric flow rate also had the effect of delaying the time to criticality. As with the bulk dissolution rate, an increase in the time to criticality was observed with a decrease in this variable. If the volumetric flow is low enough, sufficient Eu will remain to ensure subcriticality until U-235 has decayed away. However, flow rates lower that those observed today at Yucca Mountain would be required.
"Expected" Conditions
Having explored system behavior under limiting conditions, calculations based on "expected" parameters were performed. The bulk dissolution rate was set at a value of 0.001 g/m2/d. Today's flow rate of 0.001 m/yr was also used. The assumed solubilities were not changed. The reference PuO2 loading was 5wt% (as suggested by the DOE [7]) with an equal molar quantity of Eu. While the time scale is shifted into the tens of millions of years, the system does go critical at approximately 13 million years.
Stronger absorbers can and do push the time to criticality even farther into the future. (Neutronic data for Gd and Sm-149 were also used in the model.) However they too are only effective if they remain in the alteration layer. Assuming chemical behavior similar to Eu, their inclusion results in a longer period of subcriticality with an accelerated approach to criticality as the alteration layer is completely depleted.
CONCLUSIONS
The model shows that a criticality event could occur during borosilicate glass reaction in a geologic repository. Near-field criticality may occur while much of the glass remains intact or long after the glass has completely reacted. However, several approaches for addressing criticality concerns can be pursued.
The most obvious approach is to limit the Pu loading in the glass. The coupled dissolution/criticality model developed in this work predicts that if the reference borosilicate glass were loaded with 0.45 wt% PuO2, or lower, criticality would not occur. If higher loadings of WGPu are desired, Eu or other rare earths could effectively delay the onset of criticality. The model showed that relatively small amounts of an insoluble absorber can delay criticality for hundreds of thousands of years. At a minimum, REE loading should be added in sufficient quantities to control reactivity through the early keff peak that could result under worst case conditions.
Additional REE could be added to meet regulated time requirements for subcriticality when they are established. However, the conservative analysis presented here shows that even with Eu added to the glass, indefinite assurance of subcriticality presents a technical challenge for the expected Pu loading. If multi-million year assurances are needed under worst case conditions, alternate strategies may be necessary.
Backfill material used in the repository could include neutron absorbers for added control. A substance such as monazite concentrate (from sand) which has high rare earth concentrations could be used. Monazite concentrates from Florida beach sand (produced via a caustic soda process) contain about 70% monazite [8]. Of this 40% are REE oxides. Insoluble phases containing neutron poisons could also be fabricated for such a purpose. Various backfill materials should be investigated as a means for addressing repository criticality concerns.
The model demonstrates the potential importance of solution chemistry changes due to glass reaction. The rise in pH during glass dissolution increased Eu solubility. While solution chemistry will eventually revert to environmental control, the impact may be sufficient to achieve fissile/control separation. The interrelationship between bulk dissolution rate and repository infiltration rate on reaction path chemistry should also be investigated. These parameters were uncoupled in this bounding study but should be correlated to provide internal consistency in the model.
FOOTNOTES
REFERENCES