
AN APPROXIMATE-REASONING-BASED METHOD FOR
SCREENING HIGH-LEVEL WASTE TANKS FOR
FLAMMABLE GAS
Stephen W. Eisenhawer, Terry F. Bott, and Ronald E. Smith
Los Alamos National Laboratory
Los Alamos, New Mexico 87545
(505) 667-2420
ABSTRACT
The in situ retention of flammable gas produced by radiolysis and thermal decomposition in high-level waste can pose a safety problem if the gases are released episodically into the dome space of a storage tank. Screening efforts at Hanford have been directed at identifying tanks in which this situation could exist. Problems encountered in screening motivated an effort to develop an improved screening methodology.
Approximate reasoning (AR) is a formalism designed to emulate the kinds of complex judgments made by subject matter experts. It uses inductive logic structures to build a sequence of forward-chaining inferences about a subject. AR models incorporate natural language expressions known as linguistic variables to represent evidence. The use of fuzzy sets to represent these variables mathematically makes it practical to evaluate quantitative and qualitative information consistently. We performed a pilot study to investigate the utility of AR for flammable gas screening. We found that the effort to implement such a model was acceptable and that computational requirements were reasonable. The preliminary results showed that important judgments about the validity of observational data and the predictive power of models could be made. These results give new insights into the problems observed in previous screening efforts.
INTRODUCTION
High-level waste (HLW) produces flammable gases as a result of radiolysis and thermal decomposition of organics. The gases of concern include hydrogen, ammonia, and methane. Under certain conditions, it is possible for these gases to be retained within the waste for extended periods and then to be released quickly into the dome space of the storage tank. This behavior has been observed in a number of tanks at the Hanford site. It is known that in at least one such tank (241-SY-101 before it was mitigated) the concentration of flammable gases has been at or above the lower flammability limit (LFL). As part of the effort to reduce the safety concerns associated with flammable gas in HLW tanks at Hanford, a flammable gas watch list (FGWL) has been established. Inclusion on the FGWL is based on criteria intended to measure the risk associated with the presence of flammable gas. It is important that all high-risk tanks be identified with high confidence so that they may be controlled. Conversely, to minimize operational complexity, the number of tanks on the watch list should be reduced as near to the "true" number of flammable risk tanks as the current state of knowledge will support.
There are several steps in the FGWL screening process. The first is to determine if the available information is sufficient to allow a meaningful evaluation of the tank. If so, the evaluation is performed. The evaluation results in a recommendation on whether the tank should be on the watch list. Some statement of the confidence associated with the recommendation is required for this recommendation. The actual process of going from some universe of information for a tank to a clear recommendation on tank classification is a complex, frequently implicit combination of inferences about flammable gas phenomenology. These inferences about gas generation, composition, retention, and release characteristics for a tank are drawn from a large, diverse, uncertain, and often contradictory universe of information. This universe includes
It is quite common for a conclusion drawn from one set of data and models to be diametrically opposed by some other set of data and models. Data vary in terms of quality and the degree of associated uncertainty, and models have varying powers of prediction. As a result, the evaluation must contend with an entire series of qualitative judgments about what inferences regarding flammable gas phenomenology are possible and how to resolve discrepancies among them. Compounding this problem is the fact that perhaps as many as 177 tanks with widely varying waste characteristics must undergo the screening, and some demonstration of consistent evaluation is needed. This is difficult to achieve because of the wide variations in waste types and the large differences in installed instrumentation and the historical data base.
In this paper, we present an alternative to existing approaches for FGWL screening based on the theory of approximate reasoning (AR).1 Our AR-based model emulates the inference process used by an expert when asked to make an evaluation. We start with a brief history of the FGWL and the current approach to screening. We then follow with an overview of AR methodology. We briefly describe the overall logic structure of the pilot model developed for flammable gas screening. The evaluation process for an AR model is examined using one small segment of the complete model, and we show how a likelihood statement about retained gas is obtained. The computer implementation for the FGWL AR model is explained, and insights into the screening problem are presented.
FLAMMABLE GAS WATCH LIST HISTORY
A useful starting point in the description of screening methodology is to examine the evolution of the FGWL since 1990. Tanks on the original FGWL were determined using a "slurry growth" criterion based on a cursory review of tank records and supporting documents. The original FGWL contained a total of 20 tanks.2 Later, a ranking system was developed to evaluate all waste tanks in terms of the potential for flammable gas production and the potential for gas retention and release at concentrations above the LFL.3 By 1994, there were 25 tanks on the FGWL.
Inadequacies in the FGWL criteria were well known, and the then-primary contractor, Westinghouse Hanford Company, proposed new criteria in 1994.4 The criteria are based on the concentration of flammable gas needed to support combustion and the subsequent over-pressure that could be produced in a flammable gas accident. A safety factor of 4 is used. In practice, this means that to avoid watch-list membership, the flammable gas concentration in the dome space of a tank must not exceed 25% of the LFL. The factor of 4 is based on common standards for fire safety and pressure vessel design.
An effort has been under way since 1995 to evaluate all of the waste tanks against the 1994 criteria using a methodology proposed by Hopkins5 and implemented by Hodgson et al.6 Several problems have been encountered. First, the calculated gas concentration, Cfg, varies widely depending on which sensor data and models are used. For comparison against the threshold of 0.25 LFL, Hodgson et al. use max [Cfg(i)], where i denotes the concentration values calculated using discrete data/model sets. However, this preliminary comparison with the LFL is not the final screening result. An additional evaluation referred to here as the ad hoc judgment follows and is made for two reasons.
In the ad hoc step, other information or expert judgment is incorporated and a final evaluation judgment is made. Thus, much of the decision process is done "off-line" but is nevertheless an essential element in the screen being used. Note that although uncertainty in observational or parametric data can be propagated when determining max [Cfg(i)], there is no consistent method applied to represent uncertainty in expert judgment. However, the relative quality of sensors or calculational models represents the major source of uncertainty that must be evaluated by the experts during the screening process. This makes it extremely difficult to provide best-estimate/degree-of-conservatism comparisons. Finally, with the structure discussed here, it is difficult to ensure that the screening is consistent, and this poses problems during review. The considerations above suggest that the design and implementation of a new screening method should be based on a formalism that is robust and adaptable and in which all of the necessary judgments are defined explicitly. The theory of approximate reasoning provides such a formalism.
OVERVIEW OF AR METHODOLOGY
The general structure underlying the AR method described in this paper is shown in Fig. 1. We begin with some universe of information about a tank to be screened. This universe consists of both qualitative and quantitative data. This information is not necessarily in a form in which it is directly useful. Therefore, some processing of the data is required. We denote this processed data as a body of evidence, and only elements within it will be considered in the screening process. Elements of evidence must be related to each other in some meaningful manner. This is done through formal structures with logical operations relating the evidence to produce a series of forward-chaining inferences. The output from the logic structure is a description of the system called a state vector. The state vector is a concise description of a system, in this case the tank undergoing the screening. The elements of a state vector are always assumed to include some component of uncertainty that reflects imprecision or ambiguity in the knowledge of the system state. Finally, the system state vector is used in a decision model in which some definite statement about the system is made. Note that the level of abstraction increases as we move through the process. In this paper, we concentrate on how evidence is incorporated into a logic structure and how a useful state vector may be obtained.

Figure 1. Overall Structure for Approximate Reasoning Model.
In an AR model, the elements of evidence are handled as linguistic variables; that is, natural language descriptors are used. For example we can characterize the temperature in a room as "too cold," "comfortable," or "too hot" without actually measuring the temperature. The descriptors are used to define sets to which the variable of interest, in this case the temperature in the room, may belong. We say that the universe of discourse for the room temperature, T, is Te {{Too Cold}, {Comfortable}, {Too Hot}}. The sets used in AR are fuzzy. That is, a variable may belong to sets that traditionally might be considered to be mutually exclusive. For example, a temperature of 70° F could belong to both the {Comfortable} and {Too Hot} sets.
An element of information can be either quantitative or qualitative, but it is important to note that in either case, it is almost inevitably uncertain. If an element is defined numerically, it is treated as a classic random variable characterized by a probability density function. Defining the parameters in the density function then characterizes the uncertainty. Measured room temperature could be defined in this way. A qualitative element also can be a random variable. The total uncertainty associated with an element of evidence is composed of two components- aleatory and epistemic. The aleatory component represents the inherent variability in a parameter. Processes such as radioactive decay and turbulence exhibit aleatory uncertainty. The epistemic component represents state-of-knowledge uncertainty. For example, the assumptions and approximations made in a model induce epistemic uncertainty in the results. That is, there is some doubt about how well the model represents physical reality. It is important to note that in many problems, epistemic uncertainty is greater than the aleatory component.
The logic structure defines a set of relationships between the elements of evidence. The nature of the individual branch junctions depends on the particular type of relation used. A relation is a general function that maps multiple inputs into a single output. In this paper, we consider only relations with two inputs and one output. Many different types of relations , both numerical and logical, are possible. However, in our AR model, the only relation used is formal logical implication. The implications are of the form "If A and B then C" or "A and B implies C," written symbolically as (A ^B)® C. Here A and B are the antecedents. If the universe of discourse for A has i elements and B has j elements then we need i x j different implications about C to cover all the possible combinations of the two antecedents. We refer to this set of implications as a rule base. The complete form of the inference rule is
| (A is Ai and B is Bj) and (If Ai and Bj imply Ck) then Ck where k£ i x j | (1a) |
or
| [(Ai ^ Bj) ^( (Ai ^ Bj)® Ck)], Ck k£ i x j | (1b) |
This statement is a special logical construct known as the modus ponens tautology and is the basic form of rule base used in all AR models. We will discuss how such rule bases are evaluated shortly.
DESIGN OF THE FGWL AR MODEL
An important consideration in the initial development of an AR model is its scope. This determines the size of the required logic structure and is a major determinant in the amount of work required to complete the model. To illustrate the AR approach to FGWL screening, we chose to restrict ourselves to an evaluation of retained gas. There are several reasons for this. First, the body of evidence concerning gas generation and retention appears to be generally more mature than that associated with other aspects of flammable gas phenomenology. Second, the body of evidence for retention provides a diverse set of data and models that is sufficient to illustrate the ability of an AR model to combine quantitative and qualitative information and make sophisticated judgments about model validity and the resolution of conflicting results.
The parameters used in the algorithm are grouped into three general classes: predictors, enablers, and indicators. These three classes correspond to the primary modules in the inductive logic tree as shown in Fig. 2. Each class of parameters provides a distinct judgment concerning the likelihood of a significant quantity of retained gas. We refer to these likelihoods as LP, LE, and LI, where the subscripts denote the predictor, enabler, and indicator parameter groups. These three linguistic variables represent an independent evaluation of the likelihood for a significant quantity of retained gas based on a particular combination of logical inferences. Predictor parameters act as antecedents for inferences about the volume of gas that may be retained. All of the submodules used to infer LP involve one or more measurements of waste level and an associated model that combines these level data with other information to infer gas volume. Enablers are sets of parameters that, when properly combined, provide a basis for estimating the gas generation rate and the gas retention effectiveness for a tank. Conceptually, these inferences are similar in principle to those used in the early FGWL screening process. Gas indicators are parameters that can be used to infer the existence of a GRE. Positive indicators are direct measurements of an unambiguous nature, such as a dome space flammable gas concentration measurement. The absence of such positive indicators does not prove that a tank is a non-flammable gas tank. Similarly, a negative indicator has a threshold value that indicates conclusively that significant gas retention is not possible in a tank because of some distinct combination of physical characteristics of the waste and tank.

Figure 2. Rules for Combining Likelihood Judgments Based on Predictor, Enabler, and Indicator Parameter Classes.
Another important consideration in designing an AR model is determining the form in which the final output of the AR model is to be expressed. This is equivalent to specifying the format in which a subject matter expert is expected to state his conclusions. Ideally, the natural language expressions associated with the output of the model are developed in conjunction with the experts used in building it. The linguistic variable chosen for the final output in the pilot model was "likelihood of a significant quantity of retained gas". The adjective "significant" means that there is sufficient gas retention so that safety or regulatory concerns exist. We express the output likelihood, referred to as the aggregate likelihood, LF, with the following universe of discourse.
| LFÎ {{Extremely Unlikely}, {Very Unlikely}, {Quite Unlikely}, {Unresolved}, {Quite Likely}, {Very Likely}, {Extremely Unlikely} | (2) |
We will show shortly how these descriptors are used directly in approximate reasoning. The hedges "extremely," "very," and "quite" are intended to provide sufficient resolution to allow meaningful distinctions to be made and are characteristically used by subject matter experts. The set {Unresolved} is used for evaluations in which the results are inconclusive. This is equivalent to an expert saying "I don’t know" or "The data are inconclusive or contradictory." We use the expression "likelihood" in the sense that it "supplies a natural order of preference among the possibilities under consideration."7 That is, something that is said to be "very likely" is understood to have a more realistic chance of happening or to occur more frequently than something that is "quite likely." However. it must be emphasized that the likelihood linguistic variable is not to be confused with quantitative probability nor do we intend our use of likelihood to be associated directly with the likelihood function of probability theory.
ILLUSTRATION OF AR-BASED FGWL SCREENING
To illustrate the operation of an AR model, we will use a short excerpt from the complete FGWL screening algorithm. This short segment is one of the logic submodules used to infer the predictor likelihood, LP. Under the correct circumstances, the absolute level of the waste in a tank can provide information on the amount of retained gas. A substantial difference between the measured waste level and the waste level predicted by the fill/transfer history of the tank, corrected for evaporation, can be evidence of gas retention in the waste. The greater the unexplained level change, Dh, the greater the potential volume of trapped gas. This model is conceptually simple, but its application can be difficult. All waste transfers and other losses from the tank, including evaporation, must be accounted for. Given the state of the historical records, the large uncertainty in level measurements for some sensors, and the possibility of slow leaks or intrusions, calculating accurate level changes can be complex, and in some cases, the results to be inferred from it are problematic.
Hopkins4 defines the effective long-term level change to be attributed to retained gas as*
| Dh = h' - h81 +D h81+ DhE= DhM + Dh81 + DhE | (3) |
where
| h' | = the recently measured level corrected for transfers since 1981, |
| h81 | = the level measured in 1981 (used as a datum), |
| Dh81 | = the estimated gas retention level change before the 1981 measurement, and |
| DhE | = a correction to the level to account for evaporation after 1981. |
The difference between the first two terms in Eq. (3) is the measured level change denoted by DhM. The value of Dh as a predictor of retained gas depends to a large degree on how large the correction terms DhE and Dh81 are relative to DhM. If these correction terms are large, then it is reasonable to discount the importance of this model prediction. This is exactly the type of expert judgment that an AR model is designed to emulate.
We wish to draw an inference in this example about the likelihood, LDh, of a significant quantity of retained gas. To determine this likelihood, both the unexplained level change, Dh, and the quality of the data used to calculate this parameter should be evaluated. The logic structure for this evaluation is shown in Fig. 3. The three inputs are the long-term level change and two parameters, M81 and ME, used to measure the effect of correction terms on the estimate for Dh. These two parameters act as antecedents to allow us to infer a quality parameter, Q. Q and the level change, Dh, are in turn the antecedents used to infer a liklihood of a significant quantity of retained gas, LDh. This chaining of inferences is characteristic of AR models.

Figure 3. Logic Structure for Determination of Long-term Level Change Predictor Likelihood LDh.
The relative importance of DhE and Dh81 in determining Dh is represented by the parameters M81 and ME, which are defined as
| M81 = | D h 81 / DhM| , and | (4a) |
| ME = ÷ DhE/DhM÷ | (4b) |
The larger the absolute value of these ratios, the larger is the influence of the poorly known parameters DhE and Dh81.
To proceed further, it is necessary to first define the fuzzy sets in which the two correction terms may belong. In this case, we assert that both terms have membership in the same three sets: {ME,M81}e {{Small}, {Medium}{Large}}. In practice, the number of sets and the actual set linguistics are developed in conjunction with subject matter experts. The two correction terms initially will be expressed numerically, so we need a way to assign the degree of membership in each set for a particular value of the correction term. This is done using membership functions such as those shown in Fig. 4.

Figure 4. M81 and ME Ratio Membership Functions.
If ME = 3 (that is, the evaporation correction is 3 times larger than the measured level change), then ME is said to have degrees of membership, gE, in the three fuzzy sets of gE = {0,.5,.5}. That is, the degree of membership in {Medium} is g (ME, Medium) = 0.5. Similarly, a value of ME = 0.25 would imply degrees of membership of gE = {.75,.25,0}. In natural language, this might be expressed as "the evaporation correction ratio is fairly small."
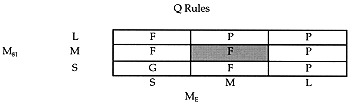
Given the antecedents ME and M81 and the fuzzy sets to which they belong, we are now prepared to define a set of expert judgments that relate them to the quality, Q, of the long-term level change prediction. We chose to use the fuzzy sets {{Poor}, {Fair} and {Good}} to describe Q, Q e {{Poor}, {Fair} and {Good}}. It is not necessary to define membership functions for Q because it is not itself an element of evidence and exists only as an internal linguistic variable. There are nine rules in the modus ponens rule base for Q; they are shown in Table I. The shaded box corresponds to the rule:
"IF the evaporation correction ratio is medium AND the Pre-1981 level change correction ratio is medium THEN the quality of the unexplained level change model is fair."
Table I. Modus Ponens Rule Base for M81 and ME to Determine Q
Referring to Fig. 3, the next inference is made about LDh using Q and the value of Dh, itself. Again, we define the fuzzy sets in which Dh may have membership: Dh e {{Very Small}, {Quite Small}, {Moderate}, {Quite Large}, {Very Large}} and the associated membership functions shown in Fig. 5. The likelihood of retained gas, LDh, is a linguistic variable that we choose to characterize by its membership in a series of sets that describe degree of likelihood:
| LDh e {{Very Unlikely}, {Quite Unlikely}, {Unresolved}, {Quite Likely},{Very Likely}} |
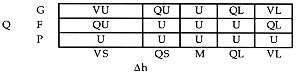
Note that this is a subset of the universe of discourse used for the aggregate likelihood LF. It should be re-emphasized that "Unresolved" does not mean "Equally Likely" but rather "No definite statement can (or should) be made." The rule base for inferring LDh is given in Table II. Note in particular the bottom row in the rule base. If the Quality is poor, then LDh always evaluates to "Unresolved." This row of the rule base deals with the situation where the quality of the data does not allow a strong conclusion to be reached with this model.

Figure 5. Long-term Level Change Dh Membership Functions.
Table II. Modus Ponens Rule Base for Q and Dh to Determine LDh
Consider now a numerical example using this set of linguistic variables, membership functions, and rule bases. For example, assume the following differential level data are available.
D
hM = 2.8 in (71 mm)D
h81 = 1.4 in (35 mm)D
HE = 8.3 in (211mm)These correspond to M81 = 0.5, ME = 3, and Dh = 12.5 in (317 mm). The degrees of membership for M81 and ME from Fig. 4 are g 81 = {.5,.5,.0} and g E = {0,.5,.5}, respectively. This means that four of the rules in Table I will be operative-the lower two rows by the two rightmost columns. We say that these four rules "fire." The firing of modus ponens rule bases with fuzzy antecedents is determined using the min-max rule. The details of the operation of this rule are discussed in Ross.8 For Q, application of the rule yields g Q = {.5,.5,0}; that is, the quality has equal membership in the {Poor} and {Fair} sets. We could express this as " the quality is poor to fair," which reflects the judgment incorporated into the rule base that if either ratio is large, then the quality cannot be good. The degrees of membership for Dh = 12.5 in are g Dh = {0,0,.5,.5,0}. That is, the level change has non-zero membership only in {Moderate} and {Quite Large}. Evaluation of the rule base for LDh using Q and Dh as antecedents with the min-max operator yields g LD h = [0,0,.5,0,0].
We recognize g LDh as a simple state vector. With this set of data, there is only non-zero membership for LDh in the likelihood fuzzy set {Unresolved}. The only possible conclusion is that the likelihood of a significant quantity of retained gas using the long-term level change is "unresolved." This agrees with the premise stated earlier that if correction terms are large, then the inference based on the long-term level change must be weak. Figure 3 shows how degrees of membership are propagated for this example as the rule bases act on the elements of evidence.
EXPRESSING THE EVALUATION RESULT
The aggregate likelihood, LF, is a random variable. This is true because most of the inputs to the inductive logic structure, such as the level measurements discussed above, are themselves random. The inescapable uncertainty in LF means that any useful statement about the aggregate likelihood will be statistical in nature. We wish to express LF in the same terms as the likelihood sets that constitute its universe of discourse. This means that a mechanism is needed to measure LF quantitatively to compute the appropriate statistics and that an additional operation must be used to express the statistical properties of LF as natural language expressions.
There is no practical way to determine the probability density function (PDF) for LF directly from the input parameters’ PDFs because the total number of inputs is large and because of the nonlinear min-max operations performed for each implication rule base. Therefore, the statistics for LF must be obtained from Monte Carlo sampling. The Monte Carlo simulation consists of N trials where for each trial, all of the input parameters are sampled from their defining PDFs and a complete evaluation is performed with these sample inputs. The immediate output from each trial is an estimate for LF that is a degree of membership vector, g LF.
At the conclusion of each Monte Carlo trial, the degrees of membership for LF in the sets {{Extremely Unlikely}, {Very Unlikely}, {Quite Unlikely}, {Unresolved}, {Quite Likely}, {Very Likely}, {Extremely Likely}} are computed. We denote this as
| LFi = g i (EU,VU, QU, U, QL,VL,EL) = [g i (Sj) j = 1,7] | (5) |
where g (Sj) is the degree of membership in set j. At the end of the simulation, we have N estimates for LF. There are two ways to calculate statistics for LF using this vector. Because of space constraints, we will restrict ourselves to the simpler approach.
It can be seen that there are seven distinct density function estimates associated with LF:
| PDF(LF) = [ PDF(g (Sj) j = 1,7)] | (6) |
We can derive the statistics from this vector. If we ask about the value of LF at some quantile qi associated with PDF(LF), we use the vector
| qi* = [ qi(g (Sj) j = 1,7)] | (7) |
This vector contains the degrees of membership at the qi quantile for each set in the universe of discourse for LF. However, note that the vector q* is not itself the qi quantile for LF. We must specify how to process the vector to compute qi(LF). A natural approach is to define qi(LF) as
| qi(LF) = max [ qi(g (Sj) j = 1,7)] | (8) |
This specification for qi is the maximum degree of membership associated with the likelihood sets at this quantile. The process of determining qi is referred to as defuzzification.
As noted earlier, we require that the result from the AR model be expressed using a natural language expression. Formally, the natural language expression of the aggregation measures is denoted as S(qi(LF)), where S( ) represents the conversion of the measure to a linguistic parameter. In the case of qi, the numerical quantity is associated directly with the set that has the highest degree of membership at this quantile. The name for this set is clearly the natural language expression to use for LF. For example, suppose that after N trials, the 0.9 quantile vector is
q*90 = [0,0,.2,.7,.1,0,0] .
Then q90(LF) = 0.7, the degree of membership associated with {Unresolved}, and the natural language expression associated with this quantile is
The likelihood of a significant quantity of retained gas at the 0.9 quantile is unresolved.
More precisely, given the PDFs for the primary inputs and the particular AR model used, the probability is 0.9 that the likelihood of a significant quantity of retained gas is unlikely or unresolved. Although S(qi(LF)) is expressed linguistically, it is not a fuzzy quantity.
The final step in the evaluation process is to compare the natural language expression with some criterion that classifies the tank. That is, we infer the classification of the tank based on the result of the inductive logic structure. This step is an example of a very simple decision model. Logically, if S(qi(LF)) ® "quite," "very," or "extremely likely," then the conclusion of the AR model is that the tank fails the screening process. This is consistent with the design of the logic structure and the definition of the output form discussed above. Similarly for the "unlikely" expressions, we conclude that the tank passes and that if S(qi(LF)) ® "unresolved," then the tank requires further study. These statements are simple implications with S(qi(LF)) as the antecedent and can be summarized as
If S(qi(LF)) is "Extremely Unlikely," "Very Unlikely," or "Quite Unlikely," then the tank passes the screening at the qi quantile.
If S(qi(LF)) is "Extremely Likely," "Very Likely," or "Quite Likely," then the tank fails the screening at the qi quantile.
If S(qi(LF)) is "Unresolved," then there is insufficient information to classify the tank at the qi quantile.
In practice, one might prefer to use different rules for classification based on degree-of-conservatism considerations. However, note that the classification decision rules are independent of the evaluation logic structure.
IMPLEMENTATION OF THE ALGORITHM
The screening model is implemented as a computer program written in the C programming language. The fuzzy rules are evaluated using a modified version of the commercial software package FuzzyCLIPS by Togai InfraLogic, Inc. The basic structure of the computer implementation is given below.
The complete AR model for flammable gas screening has 41 primary inputs with an average of 3 membership functions per input. This requires a total of 40 rulebases with approximately 12 separate rules per rule base. The AR program originally was run on an IBM PC 486-66 MHz computer with 16 MB of RAM. Running the entire algorithm for a tank required about 6 h of computing time for 2000 Monte Carlo trials. Running just the barometric pressure logic submodule required between 30 and 80 min per tank depending on the number of level sensors (one to four) that were available for each tank. On a PentiumPro 200 MHz PC with 64 MB of RAM, the run times were reduced by a factor of approximately 3.
MODEL TESTING
The FGWL model described here was developed to explore the issues associated with using an AR screening algorithm. Two of the problems considered were the following.
1. A complete tank evaluation where the entire algorithm is used. This was done for two tanks, U-106 and AW-104. U-106 is a single-shell tank with large sludge and salt cake layers. AW-104 is a double-shell tank with over 1 Mgal. of supernate. Both of these tanks had failed the screening performed by Hodgson et al.6
2. Partial evaluations using a submodule for the predictor likelihood for all of the tanks on the FGWL that had been flagged previously by Whitney.9
The first problem provides insight into the effort required to assemble the input data, the computation time needed to carry out the Monte Carlo trials needed to generate useful statistics, and the amount of effort necessary to interpret the results. Because the AR model is quite different from the approach used by Hodgson et al., detailed comparisons of the two methods was not considered practical. For the second problem, the submodule in the AR model could be compared with the Whitney model from which it evolved. A detailed discussion of the test results is beyond the scope of this paper, and only some general observations can be given here. For further detail, the reader is referred to Eisenhawer.10
One significant difference between the AR model results and those of Hodgson et al. for the complete tank evaluations involved the interpretation of the long-term level data. Both of the tanks failed the Hodgson screen based on this model for retained gas volume. However, the quality associated with the data was inferred to be "poor" in the AR model because of the large influence of the correction terms. Thus, as was the case in the example evaluation discussed earlier, the likelihood of a significant quantity of retained gas, LDh, was inferred to be "unresolved."
The correlation between barometric pressure and waste level was examined in Whitney’s analysis. If a large amount of gas is present, then with some important qualifications that must be neglected here, there should be a strong, negative linear correlation between pressure and level. Whitney examined a large number of tanks and found 37 tanks in which the correlation was found to be strong for at least one level sensor. These tanks also were examined using a submodule in the AR model for level-pressure correlation. In addition to the threshold criterion used by Whitney, additional statistical measures and judgments about data quality were used. Rulebases also were added to take into account relative instrument quality and to resolve differences between the inferences drawn for individual sensors. At the 0.95 quantile, the AR model classified 11 of these tanks as having a strong correlation and inferred that the correlation was weak for two of the tanks. Of the remaining 24 tanks that were classified as unresolved, an additional classification could be made. By observing the CDF for the output likelihood, it was possible to differentiate between tanks where the data were of reasonable quality but contradictory and tanks where the data were judged too poor to allow a definitive judgment to be made. Eleven tanks fell in this latter category. The capability to make these types of judgments explicit is an important attribute of AR.
CONCLUSIONS
Screening waste tanks for flammable gas is a difficult undertaking. The difficulty arises because of the incomplete understanding of the relevant phenomenology and the need to use partial and apparently contradictory data in models that are themselves incomplete. Our pilot study of the application of the AR methodology to this problem is encouraging. The inductive logic structure and the associated series of implication rule bases make possible a realistic representation of the current state of knowledge. The use of linguistic variables and fuzzy sets provides a way to combine qualitative and quantitative data in a consistent way. The combination of fuzzy and probabilistic approaches in the same model allows for a natural treatment of both uncertainty and ambiguity.
The pilot model showed that the effort required to build an AR model for a relatively complex problem is reasonable and that computational requirements are acceptable. Preliminary analyses with the model clearly demonstrated the value of incorporating qualitative judgments about data and models directly into the screening logic. Differences between the results obtained with the AR model and those obtained previously often could be explained as a consequence of the more detailed inferences about model and data validity included in the rule bases. We conclude that AR is a promising tool for this type of screening problem and that further development in this area would be useful.
REFERENCES
FOOTNOTE
*Other factors that may affect D h have been neglected here.