Fig. 1. Schematic of DPL Decision
Model for Frenchman Flat
G. McNulty, B. Deshler and H. Dove
IT Corp.
K. Rehfeldt and W. Fryer
GeoTrans
R. Bangerter, Jr
U.S. Department of Energy, Nevada
Operations
ABSTRACT
This paper presents an innovative use of decision analysis to perform a Value of Information Analysis that compares the cost of acquiring environmental information during a corrective action investigation with a benefit. The benefit has been defined as the percent reduction in the uncertainty of a groundwater plume boundary. The decision analysis incorporates many of the detailed elements of flow and transport modeling with some simplification. The decision model uses the flow and transport model to calculate the plume boundary, defined as the 95 percent confidence level for a 4 millirem/year organ dose, to evaluate the benefit not only of various field data acquisition and analysis tasks, but also the importance of uncertainties in the conceptual flow model. The results indicate that vertical flow, not the currently assumed horizontal flow model, may actually control the site characterization effort for the corrective action unit in question. Furthermore, the results indicate that a sizeable investment on the order of several millions of dollars is required to either resolve the likelihood of a vertical flux to the highly conductive carbonate aquifer or improve the uncertainty in the plume boundary associated with horizontal flow by only a few percent. If the new information shows that a vertical flux to the carbonate aquifer actually does exist, the boundary location may change significantly and extend well into the carbonate aquifer. The likelihood of resolving the presence or absence of this important pathway can be increased with expenditures similar to those expected for the major uncertainty reductions in the source term and minor ones in the horizontal flux.
INTRODUCTION
The Value of Information Analysis is one element of a more comprehensive groundwater operable unit corrective action strategy for the U.S. Department of Energy's (DOEs) Nevada Test Site (NTS). This Value of Information Analysis (VOIA) compares the cost of acquiring information during the Frenchman Flat Corrective Action Unit investigation with the benefit of acquiring that information; the benefit has been defined as the percent reduction in the contaminant boundary distance that can be achieved by acquiring the information. Frenchman Flat is one of the six underground Test Areas at the NTS where a contaminant boundary location will be modeled. If the boundary is found acceptable, there would be no value in acquiring additional information.
The conceptual model for Frenchman Flat assumes that regional groundwater flow and contaminant transport moves horizontally and assumes that a 4-mrem/year organ dose boundary occurs in the alluvium. Various work scope options were proposed to address key uncertainties in this model. The first and most important uncertainty to address is whether the alternate conceptual model of a vertical flux to the carbonate more accurately reflects reality. The second major concerns are uncertainties in the source term, horizontal flux, and transport properties in the base case conceptual model of horizontal flow.
The next few sections describe the basis for the Frenchman Flat conceptual model in terms of the regional flow and transport models, the decision analysis for the value of information, and results of the decision model. Specifically, we discussed what the value of information decision analysis found in terms of the relative value of the various data collection options and whether any of them should be pursued.
FRENCHMAN FLAT CONCEPTUAL MODEL
The Frenchman Flat conceptual model is based on the regional geologic, groundwater flow and contaminant transport models. A large amount of data, both historic and current, regarding geology, hydrology, source term, and other relevant information has been incorporated into these models. A regional groundwater flow model has been constructed and calibrated using available data as well as the regional geological model as interpreted input for the MODFLOW computer code (McDonald and Harbaugh, 1988). Contaminant transport modeling at a regional scale has been performed for tritium using results from the regional flow model and the MC-TRANS computer code (GeoTrans, 1995). Transport models and decision analysis used the DPL computer code (Call and Miller, 1990) to evaluate the cost of selected data collection and analysis options for reducing uncertainty in the location of the contaminant boundary. The following parameters received consideration during the additional regional uncertainty analyses of groundwater flow and contaminant transport:
Some of the parameters have more influence on model results than others. The final list of parameters emerging from the sensitivity analysis of Frenchman Flat is as follows:
The contaminant source term represents a composite of the contaminant chemistry from subsurface nuclear events at several locations. The list of potential contaminants in the source term includes other radionuclides and metals that have not yet been found in groundwater measurements. To overestimate the distance to the boundary and the relative risk from exposure to the potential contaminants, the initial quantities and the transport characteristics of the potential contaminants were considered in terms that maximized the releases. The Underground Test Area Technical Working Group (TWG) narrowed the list of possible contaminants to six radionuclides (carbon-14, cesium-137, tritium, iodine-129, plutonium-239/240, uranium-238, and lead).
DECISION ANALYSIS
Decision analysis allows the inclusion of subjective judgments. As part of this decision analysis, sensitivity analyses were performed on the regional flow and transport parameters for Frenchman Flat and on the concept of vertical flux. Such sensitivity analyses are often purporting to generate "optimal" actions on the basis of purely objective inputs. However, sensitivity analyses ignore the subjective judgements of managers and policy makers. Consequently, we need to introduce the subjective judgements of experts in how much potential field activities would reduce the uncertainty in the location of the contaminant boundary and the existence of a vertical flux. In fact, decision analysis requires personal judgements; they are important ingredients for making good decisions.
At the same time, human beings imperfectly process information; their insights about uncertainty and preferences can both be limited and misleading, even when they show great confidence. Therefore, decision analysis typically involves an iterative process that:
In this iterative process, the decision-maker's perception of the contaminant boundary may change, beliefs about the likelihood of various uncertainties may develop and change, and preferences not previously considered may mature as the decisions are reflected upon. This chapter systematically organizes the decisions that have been developed and integrates them with the sensitivities of the various flow and transport parameters and components. To quantify and integrate the individual decisions and identify an optimal information collection and remediation strategy, we used the DPL software developed by Applied Decision Analysis, Inc. (1995). The next few paragraphs briefly introduce the how this decision analysis measures the "Value of Information," how it uses DPL to tie decisions with the flow and transport calculation of distance to the contaminant boundary, and how the individual judgements of uncertainty affect the calculated distance to the contaminant boundary.
Calculation of the Value of Information
The value of a given piece of information depends on how good that information is. An expert's information is said to be perfect if it is always correct. The value of this perfect information is simply the increase in expected value that it produces:
Expected Value of Information = the expected value with information - the expected value without.
Note that perfect information is used as a basis of comparison. We know that perfect knowledge will not be achieved. Therefore, the predicted changes in distance to the boundary represent the maximum predicted changes caused by a particular piece of information.
To calculate the value of information, the sensitivity analyses of flow and transport parameters were performed with the MC_TRANS model to simplify the scope of the decision analyses by screening the list of radionuclides for consideration down to only carbon-14; these sensitivity analyses showed that the dose from carbon-14 represented the maximum extent of the boundary for the case of the six nuclides and lead. The data used in these sensitivity analyses can be described as "hard" information. In contrast, experts from the TWG assessed the uncertainty reductions based on their knowledge of the program and the subjects. They ranked the activities, and discussed how the information gained would contribute to reduction in uncertainty in the pertinent parameter, then assigned their estimated predicted percent reductions. This information can be described as "soft" information. Through the use of the DPL decision software, such "hard" and "soft" information can be combined in a systematic way to evaluate the value of various data collection and analysis options in reducing the uncertainty in the predicted distance to the contaminant boundary. This decision analysis calculates the contaminant boundary for a 95 percent confidence level for a 4 mrem/year organ dose, both of which represent assumptions that over predict the distance to the contaminant boundary. These assumptions over-predict the containment area, reduce the risk for human exposure to contaminated groundwater outside the contaminant boundary, and maximize the amount of water that is unavailable for future use.
DPL Model
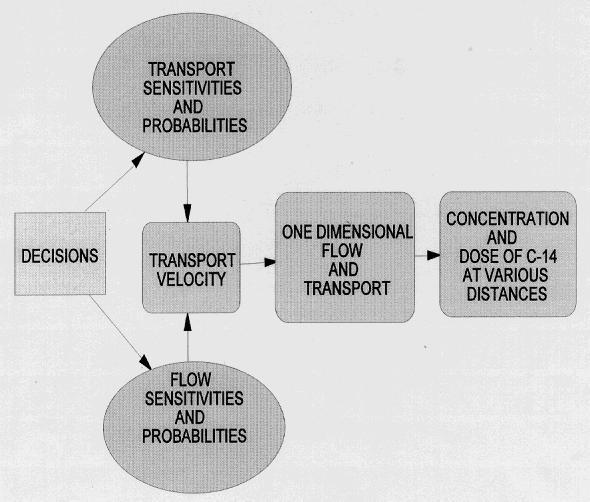
Figure 1 gives a schematic of the DPL decision model for Frenchman Flat. The rectangle represents the decisions and subjective estimates of uncertainty reduction from the panel of experts. The ovals represent the sensitivities and probabilities of values for various flow and transport parameters used with MC_TRANS. Figure 1 shows that information in the form of arrows from the rectangle and ovals goes into a calculation of one dimensional flow and transport in the first value node (rectangle with rounded corners). Note that the DPL decision model actually performs a flow and transport calculation as part of the decision analysis. This calculation uses the same sensitivities and parameter probabilities used by MC_TRANS in an analytical solution by van Genuchten and Alves (1982), the details of which are presented in the next subsection. This flow and transport calculation ultimately predicts the concentration and cumulative organ dose of carbon-14 at various distances from the source.

Fig. 1. Schematic of DPL Decision
Model for Frenchman Flat
So, Fig. 1 shows schematically how the DPL decision model for Frenchman Flat takes the "Soft Information" found in the subjective expert opinions and couples them in a Monte-Carlo manner with the "Hard Information" developed in the sensitivity analyses of the flow and transport parameters with MC_TRANS. The next subsection describes the specifics of the decision category called "Horizontal Flux" in terms of the information links among the decision rectangles, parameter ovals, and value nodes.
Horizontal Flux
The Underground Test Area Technical Working Group estimated potential reduction in uncertainty for the various horizontal flux options or decisions concerning various field tests and analysis options. DPL takes the uncertainty reductions corresponding to each decision and calculates a separate 95-percentile error band for each parameter:
Sigma95 = Std. Dev. * 2 * (1 - Uncertainty Reduction) (1)
The above equation is the key link between the "soft" information given by the TWG and the "hard" information developed in the sensitivity analyses. Through this link, DPL can calculate the transport distance to the contaminant boundary for various sizes of the error band according to the uncertainty reduction from each option. DPL calculates Sigma95 for each parameter in which a particular work alternative changes the uncertainty in its parameter. As the uncertainty reduction increases, the corresponding 95-percent error band for each parameter decreases. In the case of the average Darcian flow velocity, this would correspond to a reduction in the specific discharge components, qx and qy (The analysis neglects the effect of uncertainty reduction on qz because its value is small relative to qx and qy ). For example, DPL takes q1* (average specific discharge for the x-direction used in MC_TRANS) and simply adds Sigma95 as calculated by the above equation to yield:
qx = q1* + Sigma95 (2)
If a particular alternative gives no reduction in uncertainty, the decision model calculates the maximum 95-percentile error band for Sigma95. No reduction in uncertainty would yield the largest possible Darcian flow velocity. So, with the largest possible flow velocity, the decision model would calculate the largest possible distance to the contaminant boundary. In contrast, horizontal flux alternatives that reduce the uncertainty more would then predict smaller distances to the contaminant boundary. These reduced distances would represent the benefit of using information from those alternatives. DPL calculates the specific discharge component qy in the same way (while simply using an average value of qz, as discussed above). From these three components, DPL calculates a resultant Darcian velocity and then a seepage velocity (The seepage velocity comes from dividing the resultant Darcian velocity by the porosity and the retardation coefficient). DPL then sends this seepage velocity to an EXCEL spreadsheet that implements the one-dimensional analytical solute transport model (ODAST) originally developed by Ogata and Banks (1961) and modified by van Genuchten and Alves (1982) to calculate the concentration and dose of carbon-14 at various distances.
The solution uses a Laplace transform technique and involves products of exponential and complementary error functions (van Genuchten and Alves, 1982). The solution divides C by Co to yield normalized concentrations. Because the coefficients in the governing equations stay constant, the solution must satisfy a zero concentration gradient condition as x approaches infinity. Because this type of boundary condition is a flux type boundary condition, as opposed to the pulse concentration boundary condition used by MC_TRANS, ODAST was modified to "turn off" the decaying source at a time corresponding to the passage of the contaminant pulseout of the shot cavity modeled by MC_TRANS.
With these data, a benchmark comparison between the ODAST implementation of the pulse boundary condition and the MC_TRANS results was performed. The U.S. DOE (1996, Fig.2-4) shows that the MC_TRANS finite element code predicts that the 4 mrem/yr cumulative dose at the 95-percent level occurs at 4,500 meters at about 7,500 years, that is, the contaminant boundary for carbon-14. The DPL implementation of the ODAST model calculates a dose of 4.57 mrem/year at 7,500 years at a distance of 4,500 meters. Given that MC_TRANS is a finite element model that has included much of the geologic and flow field heterogeneity and that ODAST assumes a much simpler system, the two results are rather close.
This is not the last word on modeling for Frenchman Flat. This approach to flow and transport modeling for the VOIA simply helps define the additional work which may be needed. We have found that in comparing the MC_TRANS/MODFLOW concentrations with those of the DPL decision model, which uses the analytical solution, a difference of only 7 or so percent for Frenchman Flat. The decision analysis found that this VOIA, at least for Frenchman Flat, is not sensitive to the approach chosen for flow and transport modeling.
RESULTS OF THE DECISION MODEL
As described above, the decision model for Frenchman Flat uses the regional groundwater flow and contaminant transport data to predict the location of the contaminant boundary in the alluvium. It also uses the same data to assess what information gathering decisions will best reduce the uncertainty in the existence of a vertical fast flow path to the carbonates. The decision model for Frenchman Flat considers carbon-14 only. The dose from carbon-14 constitutes a significant proportion of the dose at longer time periods. Also, the decision model uses carbon-14 because the screening transport analyses with MC_TRANS found that for the six radionuclides (and considering lead), carbon-14 gives the largest distance to the contaminant boundary up until about 15,000 years.
The DPL model assesses various categories of work scopes (Decision Options 1 - 58, the details of which are discussed in DOE, 1997) to determine what work to collect information had the most value in reducing the uncertainty in either the existence of a vertical flux to the carbonate aquifer or the actual distance to the boundary. The first and most important uncertainty to resolve is whether a vertical flow vertical flux to the carbonate exists, because once carbon-14 reaches the carbonate, it will take relatively no time to reach the springs at Ash Meadows. Other major decisions to reduce uncertainty deal with work scopes that better define the horizontal flux, source term, and transport properties.
Within each category of work scopes, there are several alternatives that address the issue (for example, Options 25 through 58 were designed to reduce uncertainty in horizontal flux) for that category. Each option combination has a different cost and will achieve different reductions in uncertainty. The decision model takes the information a step further and combines this "soft information" dealing with subjective estimates of uncertainty reduction with the "hard information" associated with flow and transport to calculate a percent reduction in the predicted distance to the contaminant boundary. The percent reduction in the predicted distance results from the comparison of the distances predicted with and without a given piece of information acquired under a particular alternative. The next four sections give the value of the uncertainty reductions achieved for various categories of work scope and alternatives within each work scope category.
Vertical Flux to the Carbonate Aquifer
To resolve whether or not a vertical flux to the carbonate aquifer exists, we have not used DPL. Instead, we have simply used expert opinion to estimate reductions in the uncertainty concerning the existence of vertical flux to the carbonate aquifer. These data simply tell how much reduction in uncertainty each alternative would achieve in answering whether or not a vertical flux to the carbonates exists.
Table I shows that work scopes of different costs can achieve comparable reductions in uncertainty. For example, Alternatives 12, 14, and 15 reduce uncertainty between 70 and 80 percent. However, the cost among them varies from $8 million to over $12 million. Based on cost-effectiveness, Alternatives 5, 11, or 12 give the best value for the information acquired to resolve whether vertical flux to the carbonates occurs
If we assume that a vertical flux exists, we can use DPL to estimate how much the uncertainty reductions from each alternative will affect various issues related to a contaminant boundary. Because current data can be used to estimate the depth to the top of the carbonates (in contrast, we lack any data on the existence of a vertical gradient), this analysis compares percent reduction in uncertainty in time to reach the top of the Lower Carbonate Aquifer instead of the reduction in the distance to the contaminant boundary. The analyses assume a depth to the top of carbonate of 1150 meters. Uncertainty reductions in transport times to the top of the carbonate for various alternatives range from zero percent to nearly 40 percent. Most of the uncertainty reduction results because the alternatives would generate additional information on regional recharge and the porosity of the underlying units. Again, Alternative 5, 11, or 12 gives the best value for the information acquired to reduce the uncertainty in the estimated time to reach the top of the carbonates.
However, these apparently large reductions in the uncertainty of the vertical travel times have little effect on the dose at the top of the carbonates. The dose at the top of the carbonate aquifer remains at about 145 mrem/year. Reasons why the dose at the top of the carbonate aquifer seems insensitive to the data gathering alternatives for the vertical flux include:
Table I Optimum Work Scope for Key Uncertainties

None of the information derived from Alternatives 5, 11, or 12 give much practical benefit in terms of the change in dose at the top of the carbonates. Furthermore, a AT123 dilution study (DOE, 1997) suggests dilution attenuation factors of between 44 and 10 or 93 and 19 after travel through the 5,000 or 10,000 meters, respectively, of the carbonate aquifer. Even though these attenuation factors do not include the additional attenuation caused by matrix diffusion, the dose at 5,000 meters would range between 3 and 14 mrem. At 10,000 meters, the dose would range between 0.8 and 8 mrem. Therefore, with matrix diffusion accounted for, it is likely that the 4mrem/year requirement would be met somewhere before 10,000 meters.
Source Term
The strong effect of the source term upon the distance to the contaminant boundary corresponds directly to the high sensitivities described by DOE (1997, Figs. 3-1 and 3-2). Based on cost-effectiveness, Alternatives 22 and 24 give the best value for the information acquired to reduce the uncertainty in the predicted distance to the contaminant boundary. However, the practical meaning of these large reductions in uncertainty in the distance to the contaminant boundary depends upon the horizontal groundwater velocity. A low groundwater velocity would mean that these gathering information on the source term would have little practical benefit in predicting the distance to the contaminant boundary. In contrast, a high groundwater velocity could mean that the gathering of source term information would have great value in predicting the distance to the contaminant boundary.
Horizontal Flux
This category considers alternatives that measure the reduction in uncertainty by the reduction in the distance to the contaminant boundary for flow along a horizontal path. Earlier in this paper, we described how the decision model applied these reductions in the uncertainty for horizontal flux to the velocity of contaminant transport in the alluvium. The decision analysis showed two clusters of the cost/benefit results for the horizontal flux category: one cluster costs from $50,000 to $6 million to reduce the uncertainty in the distance to the boundary by 2 percent or less; the other cluster costs from $2 million to $12 million to reduce the uncertainty in the boundary distance between 3 and 6 percent. However, given these small reductions in uncertainty, neither cluster of horizontal flux options seems to have much benefit in reducing uncertainty in the distance to the contaminant boundary.
CONCLUSIONS - COST EFFECTIVENESS OF DATA GATHERING ACTIVITIES
To resolve whether or not a vertical flux to the carbonate aquifer exists, Alternative 5, 11, or 12 gives the best value for the information acquired. If we assume that a vertical flux exists, Alternative 5, 11, or 12 also gives the best value for the information acquired to reduce the uncertainty in the estimated time to reach the top of the carbonates. However, these apparently large reductions in the uncertainty of the vertical travel times have little effect on the dose at the top of the carbonates. None of the information derived from Alternative 5, 11, or 12 gives much practical benefit in terms of the change in dose at the top of the carbonates. In terms of cost-effectiveness, Option 11 for vertical flux gives a 62 percent reduction while Option 55 for horizontal flux gives only a 6 percent reduction for the same cost. So, Option 11 looks more cost-effective than Option 55 if we assume that all considerations re equal.
The strong effect of the source term upon the uncertainty in the distance to the contaminant boundary suggests that data gathering activities along this line may have considerable value. Based on cost-effectiveness, Alternatives 22 and 24 give the best value for the source term information to reduce the uncertainty in the predicted distance to the contaminant boundary. However, the practical meaning of these large reductions in uncertainty in the distance to the contaminant boundary depends upon the horizontal groundwater velocity. A low groundwater velocity, such as that believed to exist at Frenchman Flat, means that gathering information on the source term will have little practical benefit in predicting the distance to the contaminant boundary.
In conclusion, while some of the vertical flux and source term alternatives greatly reduce the uncertainty in the time to reach the Lower Carbonate Aquifer and the distance to the contaminant boundary, respectively, they both may have little practical benefit. In the case of the vertical flux alternatives, the large reductions in the uncertainty of the vertical travel times have little effect on the dose at the top of the carbonates. Estimates of the dilution potential of the Lower Carbonate Aquifer may confirm this hypothesis. In the case of the source term alternatives, the large uncertainty reductions in uncertainty may also have no practical effect because of the low groundwater velocities.
BIBLIOGRAPHY
ADA DECISION SYSTEMS. DPL - Advanced Version User Guide, Duxbury Press, San Francisco (1995).
CALL, H.J., and W.A. MILLER, "A Comparison of Approaches and Implementation for Automating Decision Analysis." In Reliability Engineering and System Safety, Vol. 30, No.1-3: 115-162 (1991).
GeoTrans, Inc., A Stochastic Advective - Dispersive Transport Code for Multiple Constituents in Dual Porosity or Fractured Geological Media. Prepared for the U.S. Department of Energy, Las Vegas, NV (1995)
MCDONALD, M.G., and A.W. HARBAUGH, "A Modular Three-Dimensional, Finite Difference Ground-Water Flow Model." In U.S. Geological Survey Techniques of Water Resources Investigations, Book 6, Chapter A1. Washington, DC, (1988).
OGATA, A. AND R.B. BANKS. A Solution of the Differential Equation of Longitudinal Dispersion in Porous Media. U.S. Geological Survey, Professional Paper 411-1. Reston,VA, (1961)
U.S. DEPARTMENT OF ENERGY. "Value of Information Analysis Report for the Frenchman Flat Corrective Action," Draft Report prepared by IT Corporation for the Nevada Environmental Restoration Project, February (1997), Draft.
VAN GENUCHTEN, M.T. AND W.J. ALVES. "Analytical Solutions of the One-Dimensional Convective-Dispersive Solute Transport Equation," U.S. Department of Agriculture, Technical Bulletin No. 1661 (1982).