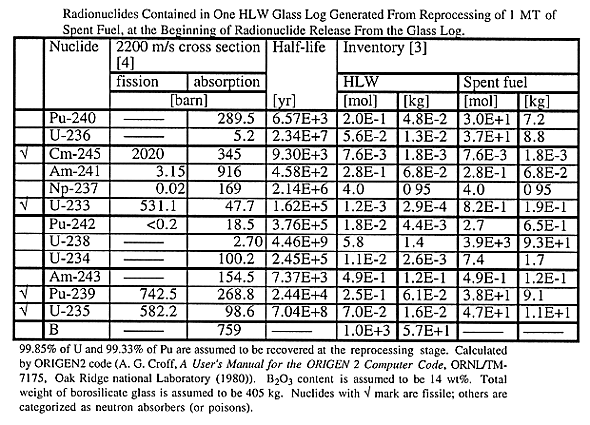
Table I Radionuclides Contained in One HLW Glass Log Generated From
Reprocessing of 1 MT of Spent Fuel, at the Beginning of Radionuclide Release
From the Glass Log.
Joonhong Ahn*, Ehud Greenspan, and Paul L. Chambré
Department of Nuclear Engineering
University of California, Berkeley
Berkeley, California 94720-1730
* Phone: 510-642-5107; Fax: 510-643-9685
E-mail: ahn@nuc.berkeley.edu
ABSTRACT
An analysis of underground autocatalytic criticality has been performed for vitrified high-level radioactive wastes arising from reprocessing of spent nuclear fuel that are placed in a water-saturated fractured geologic formation. We estimate by mass transport analyses the mass and 235U-enrichment of accumulated uranium in the host rock originated from multiple failed waste canisters, for which static neutronic analyses are performed. Uranium accumulation with 12% enrichment (denoted as U(12)) can be created. With 30% porosity of the host rock, the minimum critical mass of U(12) required for over-moderated criticality is 280 kg. Heterogeneous U(12) depositions can exhibit positive reactivity feedback due to medium temperature increase.
INTRODUCTION AND BACKGROUND
Bowman and Venneri (1) postulated scenarios for large energy releases from fissile materials buried in geologic repositories, which could occur if chemical and hydrologic processes conspire to reconfigure fissile material into an autocatalytic critical configuration. A group at the University of California at Berkeley recently completed an independent assessment (2) of scenarios of autocatalytic criticality in the proposed Yucca Mountain repository.
This paper presents preliminary results from a follow-up study which addresses a different type of waste in a different geologic set-up: high-level radioactive wastes (HLW) from reprocessed LWR fuel rather than weapons-grade plutonium or highly-enriched uranium (HEU) considered in the preceding study (2). The geologic, hydrologic and geochemical conditions considered in this study are referred to the previous performance assessment studies (3).
Because the mass of thermally fissile materials (TFM) and their decay precursors in a single canister is far less than the critical mass for the emplacement criticality, we assume a scenario that might lead to a sufficient amount of accumulation of TFM, contributed by the failure of multiple canisters. The likelihood of the scenario is unknown. We establish a mathematical model for release, transport and accumulation of TFM. Unlike the proposed Yucca Mountain repository, no specific repository site has been announced for vitrified HLW disposal. Therefore, we try to obtain theoretical worst-case predictions, by making a number of assumptions, where reliable quantitative data are not available, for the geologic, hydrologic and geochemical setting considered in the previous generic performance study (3). Even if TFM may accumulate in significant amounts, without a positive feedback mechanism for neutron multiplication, energy release by a criticality event will be insignificant. An analysis for criticality of deposited TFM has been performed.
WASTE CHARACTERISTICS AND REPOSITORY CONFIGURATION
Waste Characteristics
Spent fuel from PWR initially enriched at 4.5% with a burnup of 45,000 MWD/MT is stored for four years of cooling before reprocessing. The vitrified HLW is stored for fifty years before emplacement in the repository. The waste glass is assumed to start radionuclide release a thousand years after the emplacement.
Table I shows the inventories of relevant radionuclides in the spent fuel and HLW. Because of relatively small mass of fissile materials and large mass of boron in each glass log, the possibility of the emplacement criticality would be null. However, minor actinides, such as 245Cm, 241Am, 237Np, and 243Am, which will not be recovered by reprocessing, and residual 242Pu, 240Pu and 239Pu decay to uranium isotopes. With the inventories given in Table I, after 100,000 years, which is about four times of the half-life of 239Pu, the mass of 235U available is calculated as 0.49 + 0.25 + 0.07 = 0.810 mol. Similarly, for a sufficiently long time compared with the half-lives of the precursors, the masses of 233U, 238U, and 236U are obtained as 4.31 mol, 5.85 mol, and 0.26 mol, respectively, by lumping the initially existing masses of the precursors. With these numbers, the TFM enrichment, defined as (235U + 233U)/(236U + 238U + 235U + 233U), can be calculated as 46%. The TFM enrichment for spent fuel is calculated as 2.2%. This is the most important difference between spent fuel and vitrified HLW.
Table I Radionuclides Contained in One HLW Glass Log Generated From
Reprocessing of 1 MT of Spent Fuel, at the Beginning of Radionuclide Release
From the Glass Log.
Repository Configuration
We choose granite as a representative host rock for a repository. The repository is located under the water table (3). We assume that the geologic formation hosting the repository is characterized as a fractured medium.
Detailed repository design is yet to be determined (3). Totally 40,000 waste canisters would be placed horizontally in disposal tunnels at a pitch of 7 m. The tunnels are spaced 15 m apart. Thus, roughly 100 m2 is allocated for a waste canister, and the repository has dimensions of 2,000 m ¥ 2,000 m. The repository depth is assumed to be 1,000 m.
Engineered barriers around the cylindrical waste canister, consisting of a thick carbon-steel overpack and a bentonite-filled buffer region, is simplified as a homogeneous porous layer in this study. Furthermore, the original cylindrical geometry is transformed to a spherical geometry with equal interfacial areas. The waste canister and barrier dimensions for a sphericalgeometry are given in Fig. 1. The lifetime of an overpack is conservatively assumed to be 1,000 years (3). In the early stage of the first 1,000 years after the emplacement of the waste canister, the heat generation from a canister would rapidly decrease, and the temperature in the repository would settle down to the ambient temperature (~ 50°C). The bentonite buffer would be fully saturated by groundwater by then. Due to pyrite in bentonite and the carbon-steel overpack, the porewater in the engineered-barrier region will be in a reducing state. The hydrological and geochemical condition within the engineered barriers is assumed constant in time. Under the reducing environment, most actinide elements released from the glass log by alteration of glass matrix are hardly soluble, and will precipitate immediately. The bentonite will function as a filter for colloids. Presence of colloids is neglected in the analysis hereafter. Within the engineered barrier system (EBS), materials are transported as solute.
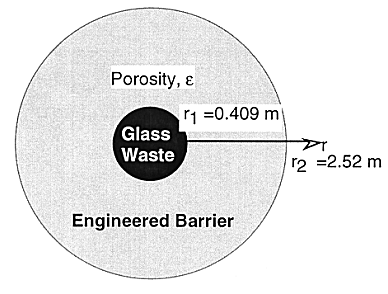
Fig. 1 Engineered
barrier dimensions.
RELEASE, TRANSPORT, AND ACCUMULATION OF ACTINIDES
We aim at obtaining the theoretical upper bound of the accumulated masses without specifying the detailed accumulation mechanisms. We assume that the radionuclides released from all the glass logs in the repository are transported to a single accumulation location, and deposited there. In the following, we consider first the contribution of one glass log to the accumulation.
Transport and Accumulation in Host Rock
Consider a rock matrix containing multiple parallel planar fractures of
width 2b, with a spacing of 2a, situated in a water-saturated
porous rock of porosity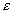 
p.
In the model for the radionuclide transport in the natural barrier, advection in
the fractures, molecular diffusion in the rock matrix, sorption onto the
fracture surfaces, sorption in the rock matrix, and radioactive decay chains of
arbitrary length are included. The velocity v is assumed to be constant with
time, uniform in the fracture. Longitudinal dispersion in the fracture is
neglected.
To estimate accumulation of TFM in the host rock, we assume that all the
radionuclide of interest arriving at a certain point a distance
far from the EBS surface will
precipitate and accumulate there. Then, the governing equation for the mass
k(t)
of the k-th radionuclide in a decay chain of length i, accumulated at z =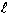 is written as
where
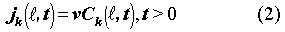
is the advective mass flux of radionuclide k at a distance
.
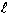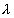k [yr1]
is the decay constant of radionuclide k. Ck(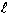,t) is the concentration of
radionuclide k in the fracture. Sf [m2]
is the cross sectional area of the fractures intersecting the repository area
per glass log. With the repository dimensions of LR X LR
[m2], the number, nw, of the glass logs placed in the
repository, and the number, nf, of the fractures
intersecting the repository, Sf is expressed as
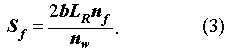
The governing equations for the concentrations Ck(z,t) in the fracture, which is needed in the solution of Eq. (1) and (2), and Ckp(y,t;z) in the pores of the rock matrix are, given by the coupled equations,
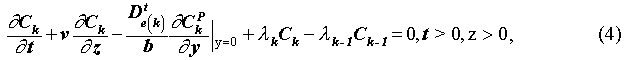
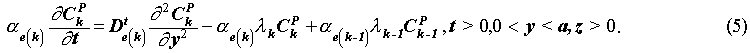
The initial and boundary conditions are:
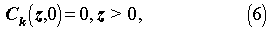
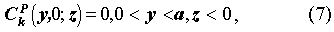
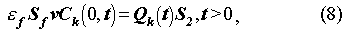
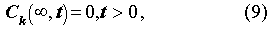
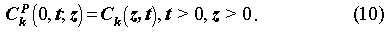
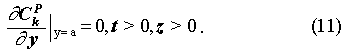
For the porous rock matrix, we define the capacity factor
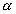e(k)
for radionuclide
k of element e as
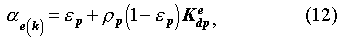
where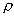 
p[kg/m3]
is the density of the porous rock matrix, and Kedp[m3/kg]
the sorption distribution coefficient of element e for the rock matrix.
Here, subscript e(k) indicates that the k-th member nuclide in a
decay chain is an isotope of element e. No retardation is assumed for
advection in the fracture.
The function,Qk(t) , in (8) is the flux of radionuclide k
from the engineered barrier, and is defined by (13). S2 is the
surface area of the EBS containing one glass log.
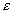f is
the porosity of the material filling the fracture.
Release from Engineered Barrier
The EBS is simplified as a single uniform porous medium, whose physical and chemical properties are represented by those of bentonite. We transform the cylindrical waste solid and bentonite region to a sphere that has the same interfacial areas. Bentonite is expected to have a hydraulic conductivity more than three orders of magnitude smaller than that of the surrounding host rock (3). Therefore, it is assumed that radionuclides are transported by molecular diffusion through the stationary water in the bentonite pores. It is assumed that the diffusive mass transport in the bentonite region has no angular dependency.
With the concentration, Nk(r, t), of radionuclide k in the water phase in the bentonite region, we define Qk(t) as
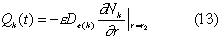
The governing equations for Nk(r, t) are written as
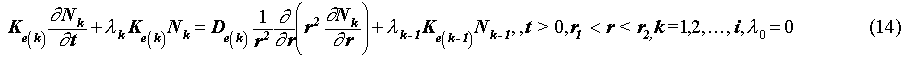
where r [m] is the distance from the center of the waste solid. r1 and r2 [m] are the radii of the equivalent-sphere waste solid and bentonite region, respectively, (Fig. 1).
The sorption retardation coefficient, Ke(k), is defined as:
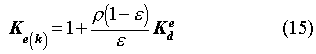
where 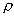[kg/m3]
and 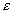are the density and
the porosity of the bentonite, respectively, and Ked[m3/kg]
a sorption distribution coefficient.
The governing equations (14) are solved, subject to the following initial and boundary conditions:
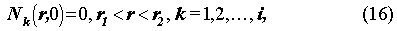
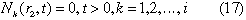
Boundary condition (17) gives a steeper concentration gradient in the bentonite region, resulting in a greater release to the host rock, than reality.
On the waste-solid surface, r = r1 (Fig. 1), if the solubility of radionuclide k is low enough, then precipitate k is created. The boundary condition is written as
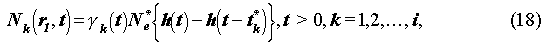
where h(•) is the Heaviside step function, N*e[mol/m3]
the solubility of element e and
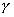k(t) the
fraction of radionuclide k in the precipitate of element e. t*k[yr]
is the time when the precipitate disappears.
If the solubility of radionuclide k is sufficiently high, then all the radionuclides released can dissolve into the water phase, and the boundary condition is written as
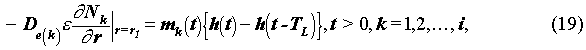
where mk(t)[mol/m2•yr] is the congruent release rate of radionuclide k. TL [yr] is the leach time of the waste solid, which is the time period between the beginning and the end of the waste glass alteration. If the glass alters at a constant rate during the leach time TL, the congruent release rate,mk(t) , is obtained by solving:
Mok[mol] is the inventory of radionuclide k in the waste solid at the beginning of the waste-solid alteration. S is the surface area of the waste glass. The solutions to (20) are readily available in (4).
To determine which boundary condition, (18) or (19), applies, the time dependent mass of precipitate k must be evaluated by considering the mass balance at the waste glass surface (Refer to (5) for the mathematical formulation). The mass of precipitates changes with time by release from the glass log by alteration of the glass matrix, diffusion away from the precipitate, and radioactive decay. The precipitate lifetime t*k is also obtained by the precipitate analysis.
We approximate 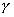k(t)
as
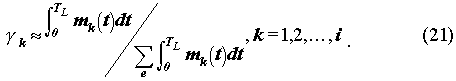
This approximation is good for long-lived radionuclides such as uranium isotopes.
Analytical Solutions
From (1), the Laplace transform for the mass,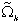
, of accumulation is obtained as
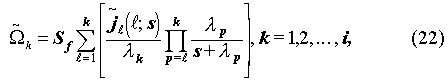
where s is a Laplace variable. The tilde ~ symbol stands for a
Laplace-transformed function. With the Laplace-transformed analytical solution,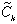
(z;s), which has been obtained
elsewhere (6), the Laplace-transformed mass flux
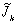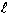(,s) at a distance
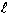from the fracture entrance
can be obtained. The Laplace-transformed diffusive mass flux
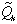is required in the boundary
condition (8). 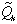can be
expressed by using the Laplace-transformed solution,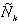
(r,s) , by (13), which has been
obtained elsewhere (5).
A computer code has been developed for the accumulation
k(t)
in the host rock. The Laplace-transformed analytical solution is inverted
numerically, based on the Talbot method (7). The readily available computer
program (8) based on this method has been utilized.
Input Data
Parameter values are summarized in Tables II and III. We make calculations for three representative cases, depending on the magnitudes of the solubilities and sorption distribution coefficients of uranium isotopes and their precursors. In case a), the upper bound values of the ranges are assigned for the solubilities of Cm, Am, Pu, and Np, whereas the lower bound value is assigned for the solubility of uranium. The lower bound values of the ranges are assigned for the sorption distribution coefficients of Cm, Am, Pu, and Np in the bentonite and in the host rock, whereas the upper bound value is assigned for the uranium sorption distribution coefficients. With such a combination, the total mass of Cm, Am, Pu, and Np existing as solutes in the water phases in the bentonite and in the host rock can be maximized, whereas the mass of uranium in the water phases is minimized. In case b), the total mass of Cm, Am, Pu, and Np in the water phases is minimized, whereas the mass of uranium in the water phases is maximized. Case c) is the median case.
Table II Assumed Parameter Values 
Table III Assumed elemental parameters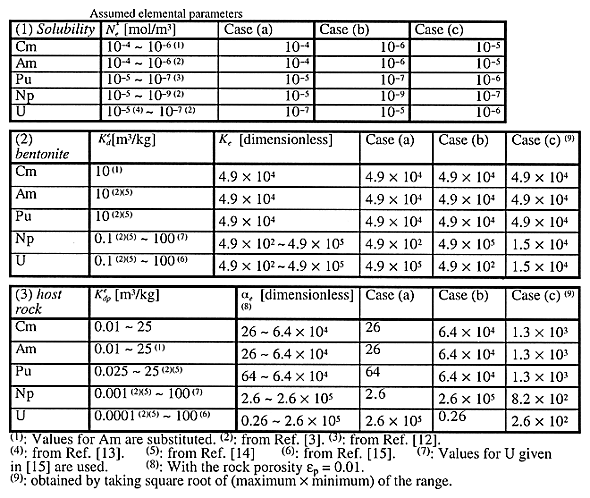 
Numerical Results
Figure 2 shows the accumulation of materials at 100 and 1000 m locations away from the EBS surface. In case a) (see Fig. 2(a-1), (a-2)), we should concern ourselves about the behavior of 233U. Because 237Np has a half-life as long as 2.14 million years, it survives the EBS transport, and is transported through the host rock, generating 233U. Uranium isotopes other than 233U cannot reach the locations beyond 100 m due to the assumed large retardation coefficient in the rock and low solubility. Because 233U is accompanied by 237Np, a strong neutron absorber (see Table I), it would be highly unlikely that the criticality configuration is realized in this case.
Suppose that the accumulation occur 10 m away from the edge of the repository area. From the comparison of Fig. 2 (a-2) with (a-1), the contribution from a glass log located at a distance greater 1000 m from the accumulation point will be negligibly small. Within a circle of radius 1000 m, whose center is located at the accumulation point, only 40% of the canisters contribute the accumulation, assuming that all the canisters fail. With a circle of radius 100 m, 0.4%, or 160 failed canisters are included. From Fig. 2 (a-1), at maximum 0.01 mol of 233U is contributed from a single glass log located at 100 m from the accumulation location. Therefore, of 40,000 canisters in the repository, 160 failed glass logs within the 100 m radius can actually contribute, and only 2 moles of pure 233U is expected to accumulate.
In case b) (see Fig. 2(b-1), (b-2)), due to the long half-lives, assumed greater solubility and smaller sorption distribution coefficients for uranium, approximately one mole of uranium could be precipitated even at the 1000 m location in the host rock, contributed by one failed glass log. The upper bound of the enrichment (235U/238U + 235U) is about 12%, but after 107 yr, the enrichment reduces to about 8%.
In case c), the accumulation starts at 3 million years at the 100 m location (Fig. 2 (c-1)). At the 1000 m location, we do not expect significant accumulation of uranium over a billion years (Fig. 2 (c-2)). With 160 failed canisters included within the 100 m radius region, only about 200 moles (5 kg) of uranium with 12% enrichment will accumulate. Therefore, in this case, the possibility of the criticality scenario will be negligibly small.
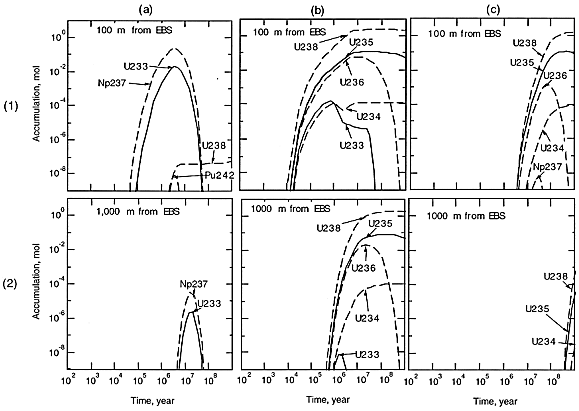
Fig. 2 Accumulation in the host rock
for cases a), b), and c). (See text for definitions of the cases) Dashed curves
represent neutron absorbers.
Thus, a case has been identified, where uranium can survive more than 1000 m transport in the surrounding host rock. Approximately one mole of uranium could be supplied from one failed glass log to the accumulation point. The 235U enrichment is found to be about 12% (we denote this by U(12) hereafter).
CRITICALITY ANALYSIS FOR ACCUMULATED URANIUM
The first question in the neutronic analysis for U(12) is what is the minimum mass required to make a critical configuration in either water-saturated silica or granite. The systems considered are reflected spherical cores of uniform homogeneous composition.
The second question is what is the minimum critical mass that is over-moderated. Suppose that a chain reaction would somehow be initiated in a critical system. As a result of the fission energy release, the system temperature would start to increase. This temperature increase would cause the water first to expand and later, possibly to evaporate. If the system were initially over-moderated, the expulsion of water would have a positive reactivity feedback that may lead to significant fission energy release.
The third question is whether there can be a heterogeneous U(12) critical configuration in which the combined reactivity feedback by Doppler broadening and spectrum hardening is positive. It is shown in (2) that the reactivity feedback by Doppler broadening for uranium systems having more than 1% 238U is negative, and that the reactivity feedback by spectrum hardening in HEU systems is negative when the HEU distribution is homogeneous whereas it is positive when the HEU distribution is heterogeneous. On the basis of these findings, we expect homogeneous U(12) systems will exhibit negative feedback by spectrum hardening as well.
The fourth question is whether homogenization of heterogeneous critical configurations of U(12) could have a positive reactivity feedback. Homogenization was found to offer a significant positive feedback in case of heterogeneous HEU systems (2).
Computation Method
The computational tool used for this study is the MCNP code (16) and its associated cross section libraries ENDF60 (which are based on ENDF-B/VI). This tool has been benchmarked against measured and calculated critical data reported upon in (17). The benchmark systems are moderated and reflected by water. Our calculated results are in very good agreement with those published in (17). The statistical accuracy of all the calculated multiplication factors is smaller than 0.5%.
MINIMUM CRITICAL MASSES FOR SYSTEMS OF UO2, ROCK, AND WATER
Table IV summarizes the minimum critical mass and corresponding spherical core radius found in the parameteric study.
Table IV Summary of Minimum Critical 235U Masses [kg] /
Core Radii [cm] for Homogeneous, Spherical, Reflected U(12)O2 + Rock
+ H2O Systems
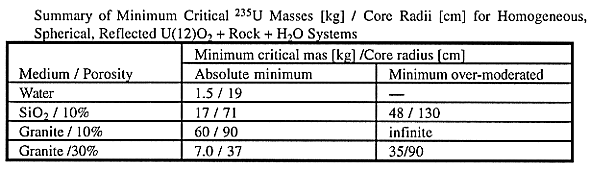
For example, the minimum critical mass is 17 kg of 235U, or 142 kg of U(12), for a spherical core consisting of uniform homogeneous mixture of U(12)O2, SiO2 with 10% porosity and water filling pores, reflected by a 120 cm thick shell of SiO2 with 0.1 g-water/cm3. The core radius for the minimum critical mass is 71 cm. For granite with porosity of 10%, the minimum critical mass is found to be 60 kg of 235U, or 480 kg of U(12). The corresponding core radius is 90 cm. The probability of accumulation of nearly half a ton of U(12) in a volume of less than 4 m3 is likely to be very small. However, the minimum critical mass for 30% porosity is as small as 7.0 kg of 235U, or 57 kg of U(12). The minimum critical mass core radius is 37 cm. This system is, however, undermoderated. The minimum critical mass in granite with 30% porosity that is not undermoderated is found to be 35 kg of 235U, i.e., 280 kg of U(12).
Reactivity Effect of Temperature Increase and Homogenization
Homogeneous critical configurations of uranium have negative reactivity feedback due to temperature increase in fuel and rock (2). Hence, we focus here on a possibility of a positive feedback with heterogeneous deposition of U(12). We consider an infinite heterogeneous lattice consisting of a one-dimensional slab unit cell made of a layer of U(12)O2 and a layer of SiO2 . The latter has a porosity of 10% and is fully saturated with water. For a 1.0 mm thick U(12)O2 layer, the rock thickness that makes the infinite lattice critical is 13.8 cm.
Table V shows the change in k of this initially critical heterogeneous lattice layer as a result of changing the fuel temperature and the rock temperature. For this parametric study, the initial amount of water was assumed to be retained, although during a criticality event a fraction of the water will leave the system by the time the rock temperature will reach 587 K or 881 K. It is observed that whereas changing only the fuel temperature has, as expected, a negative reactivity effect, the combined effect of rock and fuel temperature change has a positive reactivity effect (see the entries on the diagonal of Table V).
Table V Effect of Fuel and Rock Temperature on k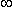
of a Lattice of 1 mm U(12)O2
and 13.8cm SiO2.
If the critical lattice consisting of 1mm U(12)O2 and 13.8cm SiO2
is mixed homogeneously, k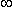
increases from unity to 1.27, 1.32, and 1.35 for the water contents of 0.1, 0.2,
and 0.3 g-water/cm3, respectively. It is also found that, for a
thicker uranium deposition layer and a greater water content, the reactivity
insertion due to homogenization is greater.
CONCLUSIONS
Possibilities for the establishment of autocatalytic criticality have been investigated for vitrified HLW buried in a water-saturated granite, based on the scenario chosen for this study. The mass of minor actinides, which eventually decay to uranium, becomes relatively important compared with the mass of uranium initially in HLW glass logs. We have found that a significant amount of uranium deposition would occur if uranium has a greater solubility and smaller sorption distribution coefficients with the host rock, than its precursing radionuclides. Due to the long half-lives of 235U and 238U, a single failed canister, which is 1000 m from the accumulation location, can supply about 1 mol of uranium with 12% 235U enrichment, although the 235U enrichment in the waste glass log is initially as low as about 1%.
The mass of 12% enriched uranium required to make an overmoderated critical system in saturated granite of 10% or lower porosity appears to be too large to be of concern. However, if the porosity is 30% or greater, then the minimum over-moderated critical mass of fissile uranium is 35 kg of 235U. Homogeneous 12%-enriched uranium critical systems can not be autocatalytic beyond a small initial power excursion, due to overmoderation. On the other hand, heterogeneous depositions of 12%-enriched uranium in saturated medium can be autocatalytic. Mixing of deposited uranium with the rock would provide another positive reactivity feedback mechanism. Thus, starting with the 40,000 vitrified HLW waste glass logs placed in water-saturated geologic formations, we can conceive of scenarios that lead to supercritical systems that exhibit positive reactivity feedback mechanisms.
The principal question would be the likelihood of such scenarios. We need to know more about the geochemical and geological conditions of the host rock to quantify the likelihood. In any case, we recommend that the criticality analysis should be added as an item of the safety assessment for the future geologic repository for HLW.
ACKNOWLEDGMENTS
This work was supported by the Power Reactor and Nuclear Fuel Development Corporation, Japan.
REFERENCES