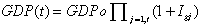 (1)
(1)
G. M. Sandquist and V. C. Rogers
Rogers and Associates
Engineering Corporation
Salt Lake City, UT 84110
(801) 263 1600
ABSTRACT
An analytical model for assessing the quantitative economic worth of a member of a given population is presented. The model employs the expected growth in population and GDP over the anticipated lifetime of an average population member. The growth projections may be based upon the past historical record for the population and its economy. US economic and population data for the 35 year period from 1960 to 1994 yield an economic worth of $3.5 million for a US population member using this model and appropriate mean values obtained from the data.
INTRODUCTION
Regulatory reform should be based upon quantitative risk analysis, and risk analysis of any kind should be based upon objective and unbiased scientific and economic data and observations. Furthermore, incremental risk reduction and other benefits should be clearly related to incremental costs. Risk analyses and assessments for waste management and remedial actions must quantify the risks of morbidity and mortality imposed upon the members of a given population to be objective.
A major element of this quantification effort is rationally assigning an economic value for a human life. There are many economic measures for human morbidity and mortality that have been assigned with some quantitative basis by governmental agencies, scientific groups and others. Ref. 1 provides over 500 estimations of the economic cost of a year of life-savings for a broad range of risk categories. For example, the median cost for medical intervention is $19,000 per year of life, while the cost for injury reduction is $48,000 per year of life and $2,800,000 per year of life for toxin control. These sample costs differ by a factor of nearly 150 per year of life saved. The median cost is $42,000 per life-year or about $3.2 million for a 75 year life estimate for all risk categories reported.
A quantitative model is developed and evaluated here for unambiguously assigning an economic worth to an average member of any economically definable human population if certain characteristics about the population and its economy are known. The model is based on the effective per-capita gross domestic product for the population group and its anticipated variation with time.
MODEL
Assume for an identifiable population group that the effective gross
domestic product or GDP ( the total economic value of all domestic goods and
services produced by the group) vary with time according to the following
discrete expression
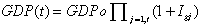 (1)
(1)
where
GDP(t ) = value of GDP at any discrete time period for t > 1
GDPo = value of GDP at reference time t = 1
Igj = rate of change of GDP at time period j
t = discrete time period (e.g., years) from reference time period t > 1
For this same population group assume that the change in population membership for a given time period is given by the following discrete expression
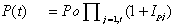 (2)
(2)
where
P(t ) = number of members in group population at any discrete time period t > 1
Po = number of members in group population at reference time t = 1
Ipj = rate of change of group population at time period j
Now for any discrete time period (e.g., annual period) for the population under study the economic worth of any member is assumed to be that mean share of the GDP contributed by the member of that population. This worth changes with time with changes in both the GDP of the group population and the change in the membership of the group population with time. Summing this period (annual) worth over the expected lifetime T of the average population member gives the mean economic contribution of an average individual to the total economic worth of the group population for the time period T. Thus, an estimate of the economic worth of an average member of this group population is given by the following:
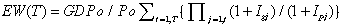 (3)
(3)
where summation over time is performed for a mean lifetime, T, of the average group population member.
This mathematical statement for the economic worth (EW) of a human life in that group population is equal to the time averaged GDP per capita generated over the mean lifetime of a member of the population. The economic contributions associated with the external environment (land, unexploited resources, and other non-GDP measured resources and values) are not included in this estimate for the EW. Only the tangible, measurable economic value arising from the groups' members productive goods produced and services rendered are attributable to the worth of the individual in the group.
A integral expression for EW can be also be formulated for time as a continuous variable and GDP(t ) and P(t ) as continuous functions of time as follows as developed in Ref. (2)
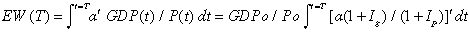 (4)
(4)
and
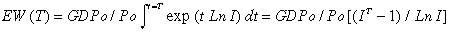 (5)
(5)
where
I = a (1+Ig) / (1+Ip)
GDP(t ) = GDPo (1+Ig)t
P(t ) = Po (1+I p)t
GDPo = value of GDP at reference time t = 0
Po = number of members in group population at reference time t = 0
Ig = mean annual rate of change of GDP over time interval 0 < t < T
Ip = mean annual rate of change of group population over time interval 0 < t < T
t = time in years from reference time t = 0
T = average lifetime of group member or years of life lost.
a = the effective population / GDP adjustment factor over time interval 0 < t < T where 0 < a <
Observe that if a = 1, no time adjustment is imposed upon the time dependent GDP or population distribution. For a > 1 the time adjustment increases monotonically with time, while for a < 1 the adjustment decreases monotonically with time. Also if I = 1 in Eq. (5) then EW(T) = GDPo T /Po
To investigate the utility of these models, official US economic and population data was used as a data base. Table I provides the essential data required during the past 35 year time period to determine economic worth estimates for US citizens based upon assumptions of the model. The data source is the "Economic Report for the President" by the Council of Economic Advisors, dated February 1996. All dollar figures are real and are inflation adjusted to 1992 dollars. Table I provides annual values for 1960 through 1994 for US population, the annual percent increase in population, the GDP and annual percent increase in GDP, the annual GDP per capita, and the mean lifetime expectancy of a member of the population. Finally, the principal parameters employed by the model, namely the annual effective ratio of economic to population growth ratio I, and the economic worth of a population member EW are given in the Table.
Table I Data for Evaluating Economic Worth of US Population Member
(1960-94)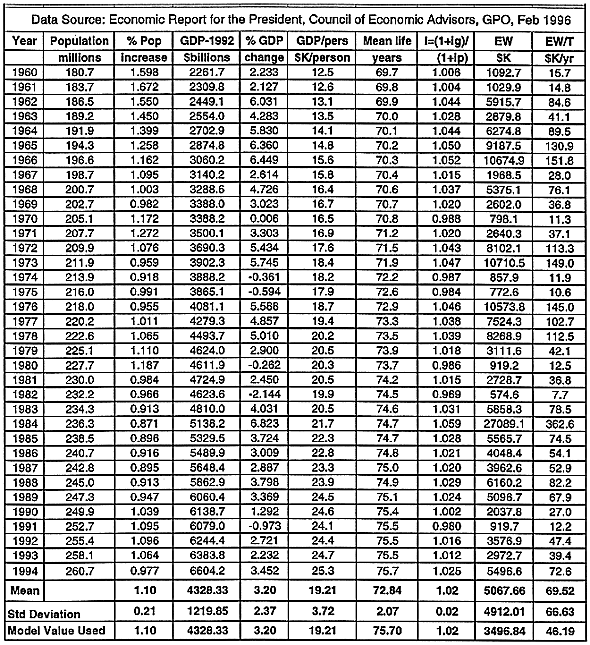
For the US population over the 35 year period of 1960 through 1994 the following values are employed from Table I to demonstrate the economic worth model and the averaging process for the year 1995 adjusted to 1992 dollars. The average GDP per capita is used (1960-1995) with the 1994 population to obtain the effective GDPo. The effective ratio of economic to population growth rate I is obtained from the 35 year averaged population and GDP annual changes.
GDPo = $ 6604 x 109
GDPo/person = $19,210 (35 year average)
Po = 260.7 x 106 persons (1994 population)
I g = 3.20 % (projected annual future growth rate of US GDP)
I p = 1.10 % (projected annual growth rate for US population)
a = 1 (no time adjustment)
I = 1.032 / 1.010 = 1.021 (35 year average)
T = 75.7 years (expected mean US resident lifetime as of 1996)
EW = $19,210 x [{(1.021)75.7- 1} / Ln (1.021)] = $ 3.5 million
It is found that EW = $3.5 million, which is the models quantitative estimate of the economic worth of average member of the US population as of 1994 with appropriate mean values used over the 35 year time period 1960 through 1994. The value of EW represents the economic loss incurred by the absence of an average member of the US population based on this model. Averaged over the US population mean lifetime for the year 1994, the average annual economic loss is about $46,000 per year which is similar to the median value given in Ref. 1. This example indicates that the use of real economic and demographic data can be utilized to provide a quantitative estimate of economic worth of individuals in an economic group which is in substantial agreement with the perceptions and estimates of numerous societal, economic and occupational groups. However, it is important to observe how sensitive the model is to the estimated growth rates for both the GDP and population. For example, for the US during the period 1960 to 1994, the EW value assumes a maximum value of $27.1 million in 1984 and a minimum value of $574.6 thousand in 1982. Utilizing 1994 data, the EW from Table I is $5.50 million while the 1993 value is $2.97 million. Thus, it is obvious that appropriate averaging of the economic data for a population group is required to make the quantitative model useful and reasonable when projecting the economic worth of a population member over an expected lifetime.
CONCLUSIONS
Besides the population GDP as an indicator for a measure of economic worth of a given population member, there are other economic indicators that could be used such as the total wages and earnings for the working population. The quantitative model for the economic worth of a member of a given population group presented here is based upon the GDP which is a measure of the economic value of all goods and services produced by the group. These economic data along with population statistics are usually carefully monitored and reasonably accurate for most distinguishable population groups. Finally, the model presented here is objective, quantitative and defensible and can be readily applied for assessing economic consequences associated with waste management risks.
REFERENCES