 (1)
(1)
P.L. Kunsch and D. Emmery
ONDRAF/NIRAS
Place Madou
1 POB 25
B-1210 Brussels (BELGIUM)
ABSTRACT
The paper gives a qualitative overview of the advanced cost-benefit analysis based on the option value methodology. This methodology, first developed in finance and applied to profit-oriented firms, is equally valuable for a state-owned radwaste agency committed to non-profit aims. We first show why the traditional Net Present Value technique (NPV) fails to define adequate timing in the starting date and in the completion schedule of irreversible investment decisions to be made under uncertainty. The option approach, on the contrary, gives a tool for coping with the uncertainty in a flexible way. Two main sources of uncertainty are considered. The first, input cost uncertainty, affects the amount of resources necessary to complete a project. It can be resolved by observing the cost evolution. The second, technical uncertainty, relates to the imperfect knowledge of actual costs. It can be resolved by realizing the project. We illustrate the use of the methodology by a qualitative discussion of several decision processes related to radwaste management projects.
Keywords : investment decision, option value methodology, input cost uncertainty, technical uncertainty
INTRODUCTION
In traditional capital budgeting analysis of a commercial organization, investment and financing decisions for new infrastructures or facilities are based on the Net Present Value technique (NPV). NPV is the main instrument of Cost-Benefit Analysis (CBA) considering the time dimension of the cash flows of costs and benefits generated by potential projects. Imposed constraints are the firm's capital structure and the internal rate of return.
Recent advances in financial theory have shown that the CBA technique is inadequate in the presence of important uncertainties attached to irreversible decision processes. There is now a fast growing literature showing that the value of options for abandoning or starting a risky and irreversible project must be incorporated into the streams of costs and benefits (see Pindyck (1), and for an overview Dixit and Pindyck (2)). The option value techniques have therefore become part of CBA in an advanced sense for decision-making under uncertainty.
The state-owned radwaste agency which is operational in Belgium is not a commercial organization. For the sake of being simple, we will call it in the following the "agency". Nevertheless we try to demonstrate that option-based CBA approaches are relevant whenever investment decisions are pending. We start by demonstrating in the following section the way traditional CBA has been applied, and why it is not satisfactory. In the next section, we show how the value of options is taken into account in the advanced CBA approach. In the forelast section, we discuss the qualitative use of this technique by the agency, by presenting typical investment decisions under uncertainty. Finally, we draw the conclusion in the last section.
TRADITIONAL CBA IN WASTE MANAGEMENT DECISION-MAKING
The radwaste agency of the Belgian type is supposed to be completely autonomous in its investment decisions. While this can be considered to be a favorable position, it puts rather tight constraints on the financing capability of the agency. The agency does not have its own capital. It works according to the "polluter pays principle" (PPP) at cost price, i.e. without making losses nor profits on the waste management operations. Project financing must therefor rely on down-payments made by the producers, and set aside as provisions in dedicated accounts or asset portfolios. In the present analysis, we will only consider investment projects with the following characteristics :
In principle the down-payments are made on the basis of per-unit tariffs charged on each volume of waste entrusted to the agency. The determination of tariffs is based on the methodology called "reservation of capacity" described in a previous paper (Kunsch and Emmery (3)).
We briefly illustrate the approach based on NPV calculations.
Assume a cost stream C(t) for the project, a waste quantity M, and an average rate of return r on assets. The initial tariff T(0), supposed to be applicable to the full quantity delivered in year t=0, can be calculated by equating the NPV of revenues to the expenses, as follows :
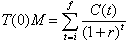 (1)
(1)
where i and f are the initial and final investment date respectively.
The tariff T(t), applicable to waste delivery in year t, is then yearly updated
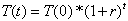 (2)
(2)
assuming that t<i to avoid the complication of having to borrow additional money at a rate superior to the rate of return r.
As the agency has no internal rate of return, a low value of r can be chosen to limit the risk of insufficient revenues. r=0% would be chosen if the total cost is thought to have a systematic upward trend equal to the average return rate.
In theory, the NPV formula has the following double purpose :
A prudent and apparently rational recommendation is first to fix a tariff level which is thought to be readily accepted by the waste delivering organizations. Secondly to wait until the balance of provisions with costs has been established before starting the investment. In real world conditions, however, the exact timing will only be determined ex post, as waste collecting revenues and exact costs are not known ex ante. In case of rough underestimates in both incoming and outgoing cash flows, the decision would be postponed in an unpredictable way, in some cases forever, as no risk of uncovered overcosts can be taken.
Under real world conditions, traditional CBA is not an adequate decision instrument for the agency. There is an obvious reason why it should be so. In fact the provision collecting agency can be considered to be a reverse image of the profit-oriented business. It generates positive cash flows prior to the investment decision. It is why the decision of starting a new risky project can never be dictated by the NPV analysis alone. Even allowing for stochastic changes in costs streams, waste quantities and asset returns would not basically change the non-adequacy of this technique. The decision will deprive for certain the agency from its provisions instead of increasing them. The mere financial rationale commands therefore to wait before investing irreversibly in any risky project.
In short, genuine timing is not part of CBA, which is a completely static approach. The more careful analysis of the uncertainties in the agency's projects reveals that more adequate timing recommendations can be obtained using modern option value theory. In the next section we briefly present the main elements of this analysis.
UNCERTAINTIES AND THE ADVANCED OPTION-BASED CBA
To describe the option value methodology, which can be used in quite a broad context, we will restrict our vision to the point of view of the agency when it deals with a not yet specified uncertain project. The characteristics of such a typical project have been enumerated above.
To make our point clear, we will make some simplifying assumptions which can be removed at the cost of analytical complications on which we do not wish to focus. Interested readers will find more details in a forthcoming paper and in (1, 2).
First, as the purpose of the agency is not to make profits, we will assume without loss of generality that the rate of return is r=0% in real terms. In practice, the agency has adopted a risk-free rate of interest r=2% in real terms. For the sake of explaining the r=0% value, the assumption is made that this return is exactly compensated by the systematic upward trend in the project costs.
Secondly, as the purpose is to concentrate on the aspects of costs uncertainties, it will be assumed that the revenues generated by the down-payments are available in their totality prior to the decision, and that they are therefore perfectly known. The applicable tariff may have been the result of a compromise between risk calculation elaborated from Eq. (1) and negotiations with the waste producing organizations providing money to finance the future project.
The decision to be taken is then reduced to the point of defining when to start the investment project and in within which period it should be completed.
Call now K the total project's investment. K is here a random variable. Because the project needs time to be completed, we assume that the yearly maximum investment rate is constant and equal to I. If the investment is completed at the maximum rate of I per year, it would take a minimum random time of
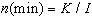 (3)
(3)
We now adopt the terminology of Dixit and Pindyck (2) to discuss the nature of uncertainties affecting the project cost K. Many long-term projects suffer from two basically different sources of uncertainty. Examples are to be found in large petrochemical complexes, the development of a new airplane, in the construction of a nuclear power plant, and also - and this will be the case in the paper - in radwaste handling facilities.
The first uncertainty type is called input cost uncertainty by Dixit and Pindyck (2). It arises because the basic costs of material and manpower are fluctuating. In addition, and this can become acute in radwaste projects, safety or environmental regulations may change, requiring the use of more capital or resources in the basic inputs. Because the project cost K is fluctuating, the question is to know when to start it.
Let us assume that the known value of the project is represented by V, which is equal to the cumulated value of down-payments.
As an example, suppose that n=1 (project completed in one year), and that I is 100 today, but next year it could increase to 110, or decrease to 80, each with probability 0.5.
Assuming that V=100, which decision should be taken today?
The NPV of a decision today is therefore given by
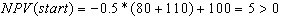 (4)
(4)
the non-negative value of which is in favor of immediate investment.
However this approach misses an opportunity : to make an observation one year later, and then to know for certain the cost at that time.
If I=80, the investment will take place. If I=110 it will be abandoned or replaced by a another project at a later time. Taking this option to realize the investment one year later gives the following NPV
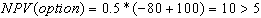 (5)
(5)
as the probability of exercising the option will be 50%.
The option value (OV) is represented by the difference in the NPV's equal to OV = 5. Because it is positive, the waiting alternative should be preferred.
The second type of uncertainty is called technical uncertainty by Dixit and Pindyck (2). In the first type of input cost uncertainty described above, new information is revealed independently of what is being done by the decision-makers. Technical uncertainty, on the contrary, will be only lifted by realizing at least part of the project. This is the result of new experience gathering thanks to the principle "learning by doing". This type of uncertainty, when present, would therefore tend to accelerate the investment decision.
Let us suppose as an example that I=40, while V=100, but that there is a probability of 0.5 that after the investment has been done, an additional amount of 200 has to be spent due to technical difficulties.
At first sight, it may seem that the NPV= -40 + 100 - 0.5*200 = -40, being negative, might prevent from investing now. But this ignores the learning experience obtained by realizing the project, and the option of abandoning and replacing it by an equivalent project should extra costs of 200 be necessary. Considering this option gives the correct NPV = -40 + 0.5*100 = +10. It is positive, so one should invest without waiting. Here we have OV = 10 -(-40) = 50 >0.
Both technical and input cost uncertainty affect the value of an investment opportunity. In general, however, they affect the decision differently. Technical uncertainty makes investing more attractive as learning by doing will reveal more information about the actual costs. On the other hand, input cost uncertainty has in general the opposite effect, because there is a value in waiting for new information. In most decision problems, both types of uncertainties might be present, and it is important to account for their antagonistic effects. However, one or the other type of uncertainty often dominates. In radwaste management we have found that typical decision problems can be identified for both types of uncertainty. For example, the decision to implement a shallow-land disposal facility for low-level radwaste will be dominated by input cost uncertainty. Elements of technical uncertainty will be found in other decisions, like implementing alpha-waste conditioning facilities, or decommissioning a nuclear research reactor.
Before we come back to these examples in the next section, we briefly give a more general description of the option methodology. It is compared to the traditional NPV methodology in Fig. 1. Note from that figure that a first basic difference is that NPV lacks any flexibility as the decision making is completed in t=0. In the option methodology, on the contrary, the decision may be revised in each year t.

Fig. 1. Comparison between the two
methodologies K1,K2=some values of the current project cost K; V= Value;
K*=critical cost; I=yearly investment rate
Let us call as above K the fluctuating cost of the project, and k < I the yearly investment rate, bounded by the maximum constant value I. K is not known, being a random number; only its average value E(K) is known. The decision problem consists in defining in each year t an investment strategy k(t), such that the opportunity to invest is at its maximum.
In optimization theory, using dynamic programming, it can be shown - under quite general assumptions regarding the random behavior of K - that in each year the investment rate k(t) is either vanishing or at its maximum equal to I. Indeed k(t) will be vanishing as long as the cost is superior to some critical value of the cost K*. I.e.
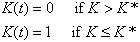 (6)
(6)
The K* value will depend on the parameters defining the random behavior of K. In case the option value is positive, the critical K* will exceed the project value V (Note from Fig. 1 that the NPV formula imposes to have the cost K being below the value V, i.e. the critical cost K* = V, because there is no option value).
The interpretation of this formula is quite clear. Should the fluctuating cost exceed some critical threshold, the investment should be discontinued, and k(t) = 0. If, on the contrary, the cost remains below K*, investment should go on at the maximum rate, and k(t) = I.
It is now an interesting general result that K* will be increasing with the degree of technical uncertainty, while it will be decreasing with the degree of input cost uncertainty. In addition K* will be much more sensitive to a change in the latter uncertainty.
Again the interpretation of these findings is clear : the more technical uncertainty there is, the greater the value of the opportunity to invest OV (Option Value) will be, and the larger the maximum expected cost for which starting to invest is economical.
On the contrary, if input cost uncertainty is large, the investment opportunity will be decreasing, and so will the cut-off value eliminating unattractive projects. However, this depressing effects on investment, due to the increasing need for resources, will be far less rapid than in the previous case.
We now illustrate qualitatively these results using the quoted examples from the agency's experience.
EXAMPLES FROM THE AGENCY'S EXPERIENCE
The option approach briefly developed in the previous sections has been particularly useful in several instances. It proved not only an adequate tool to ease difficult decisions, in particular regarding the aspect of proper timing, but it also provides useful insight into the unfolding of specific decision processes. Regarding the latter aspect, Dixit and Pindyck (2) claim to understand why so many nuclear power plants have been abandoned before operation in the U.S.A. due to input cost uncertainty.
In the particularly difficult case of the siting of a shallow-land disposal for low-level waste, the analysis has without any doubt provided some insight into the intricate, and not yet successful decision process. While the technical project can be now considered quite mature in Belgium - a preliminary study has been published in 1994 - little progress has been made in the last two years. Similar projects are now operational in France and Spain, and it can therefore be considered that technical uncertainties are few. The main reason for delaying the investment has been the important input cost uncertainty. The origin of the latter is found in the unpredictable result of the search for a suitable site. Note here that Belgium is one of the smallest countries in Western Europe, while it has a very high population density.
At the very start of the process, it was not known with any confidence how important a commitment and use of resources would be necessary to be successful in the quest for a suitable site. It was to be expected that the local population and their municipal authorities would request a rather high price to share the presence of such an unpopular facility. The interest of future generations was unlikely to influence favorably the balance between responsible behavior and refusal or fear of such project.
The very nature of this uncertainty dictated to the agency to first acquire a correct measure of the resource involvement that would be necessary to succeed. This approach is in complete agreement with the recommendation of the option-based approach as discussed in the previous section, in the case of input cost uncertainty.
The agency applied this strategy in 1994-1995. This is not the place to discuss the suitability of the chosen approach for assessing the level of public acceptance with respect to the project. In any case, this process triggered a fierce upsurge of refusal from most municipalities in the country. This heavy reaction proved that the actual social cost of the project was considerably higher than the estimated technical cost. More precisely, the total cost K exceeded largely the critical cost K* and it was not at the time adequately covered by the planned level of resources V (see Fig. 1). The recommendation of the option approach as felt intuitively by the agency's management was therefore to block the project for immediate investment.
Following this first step, three alternative options are now open to the agency. Each depends on the future beliefs of its management regarding the siting project :
Should the first stage not be successful, the agency still has the opportunity to abandon the project at low cost, and to move to alternative 1.
The authors believe that this last approach is the most rational one. In a previous paper on this issue (Kunsch et al. (4)), one of the authors argued that only a timely decision can prevent a project of this type from abandonment as provided for option 1.
A second case we wish to present is the handling and conditioning of alpha-bearing waste, coming mainly from MOX manufacturing or from fuel reprocessing in the former Eurochemic plant in Dessel. The decision to invest in a suitable facility is made difficult by the presence of mainly technical uncertainties. Although there are also some regulatory aspects which might ultimately affect the input costs, we choose to ignore them in this simplified discussion. As said above, pure types of either technical or input cost uncertainty only exist in theory, but dominant characteristics can be identified in many practical problems.
There are several reasons why the costs of a convenient facility for handling and conditioning alpha-bearing waste forms are uncertain (De Grauwe (5)):
The agency has three alternative options :
We think that a flexible and at the same time responsible strategy requires the latter approach.
A similar decision path is applicable to the decommissioning of the BR3 PWR reactor located on the site of the national research center CEN/SCK in Mol (Braeckeveldt and Schrauben (6)). Put into operation in 1962, with a net electrical output of 10 MWe, it was shut down in 1987. The funds for its decommissioning are provided by the Belgian state, with the support of the European Commission which selected it as a pilot project to gain experience for the decommissioning of power reactors. Technical uncertainty is important due to the use of highly enriched Pu-fuel during the operational period and the resulting contamination and activation of internals, making it difficult to assess the costs.
The first phase of the project is currently underway. It involves the chemical decontamination of the primary loop and the selection and testing of tools for remote dismantling of the reactor internals.
The second phase will cover the actual remote dismantling operations.
From a traditional cost-benefit point of view, there are seemingly many reasons why this second phase could be delayed (MacKerron (7)). These reasons are first dictated by technical arguments, like the reduction of activity levels which brings in turn a reduction in the difficulty and expected costs of the dismantling process. The financial argument of cost discounting is also part of the debate as a proper timing. It is difficult to imagine any traditional cost-benefit argument which is in favor of timely actions.
The option-based model, however, shows how the pressure to learn from experience counteracts the postponement trend. Recourse to arguments of purely ethical nature are then superfluous to impose a timely decision, although ethics dictate why decommissioning must eventually take place within a reasonable period (abandoning the project is clearly not acceptable here). As in the alpha-bearing waste issue, the use of the option methodology delineates the need for experience to depress the initial technical uncertainty.
The preferred option is to start the second stage as soon as possible, keeping the flexibility of discontinuing subsequent actions under financial or technical constraints, such as the momentary absence of a disposal site for highly activated components.
CONCLUSION
The basic and rather simple idea behind the option value methodology is to add flexibility to the execution of irreversible and uncertain investments which take time to complete. This tactical flexibility consists in exercising options at each stage of a given project for starting, discontinuing or abandoning it when acceptable, whenever critical boundaries of the "costs" are crossed. Note that "costs" in an extended meaning may include non-monetary resources like public acceptance or regulatory levels. The traditional NPV approach, on the contrary, fixes ex ante the full investment path and is completely rigid.
A state-owned agency such as ONDRAF/NIRAS is confronted with difficult timing decisions which benefit from the potential of adaptative strategies. We have brought some examples from our experience, refraining from going too far into formulation details. We think that bringing this new methodology to a fully operational stage, also quantitatively, would represent a valuable step toward a still more responsible decision-making process.
REFERENCES