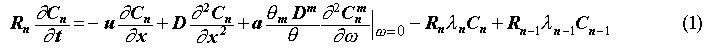
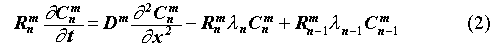
M. Andersson, B. Mendes and A. Pereira
Dep. of Physics,
Stockholm University
Box 6730
S-113 85 Stockholm, Sweden.
email:
marlene@grub01.physto.se, mendes@physto.se, antonio@vanfp4.physto.se
ABSTRACT
The impact of the heterogeneity of fractured media on the risk estimations obtained from a radionuclide transport model is studied. The model used is the CRYSTAL3D model, which has been developed for use in probabilistic assessments. CRYSTAL3D is used as a submodel of a parallel Monte Carlo driver now under development for the GESAMAC project. Case calculations have been done for 243Am. They confirm previous results concerning the effect of heterogeneity along the nuclide transport pathway. Peak releases tend to decrease, as does the variance of the output distribution of the consequences, i.e., the uncertainty results are narrowed for the peak distribution due to the averaging of properties along the pathway.
The downside for increasing the realism of the model is two-fold: first, one needs high- performance computing resources, and second, extra complexity is introduced in the sensitivity analysis of the results. In our sensitivity analysis the parameter distributions have been reduced to single numbers, in this paper, to median values which make it possible to apply the usual sensitivity analyses methods to rank the importance of the geosphere parameters.
A preliminary evaluation of the performance of the parallel Monte Carlo driver shows very satisfactory results.
INTRODUCTION
In the estimation of the long-term risks associated with radioactive waste repositories, a wide spectrum of models is used. In the first step of the computations in a PA assessment, hydrogeological calculations are done, in two or three dimensions, to evaluate parameters like residence time, longitudinal dispersion or the Darcy velocity field. This information provides input parameters for the transport models in the second step. Transport model calculations are aimed at the estimation of long-term risks to man and other biota from contaminant releases. In the transport models the influence of chemistry is taken into account by modelling those phenomena that are known to be of importance for transport, like radionuclide sorption on the fracture walls, diffusion into the rock matrix, radioactive decay and influence of colloids and complexation. In résumé, a stepwise approach is commonly used in PA assessments, the hydrogeological calculations being decoupled from the solute transport calculations.
In the two steps mentioned above groundwater flow is of paramount importance. The mechanism of groundwater flow in fractured media like crystalline rock, varies considerably from that in porous media. This aspect reflects upon the two types of heterogeneity characteristic of fractured media. The first one is of geometrical character and is related to the complex pattern of fractures with different forms, lengths, apertures and orientation in space, constituting a network of channels, some of them providing fast pathways for radionuclide transport, others forming dead ends. The second one is associated to the variability of physical and chemical properties along the transport pathways as a consequence of the mineralogical composition of the fractures walls and of the rock mass in general.
In this paper we address the impact of heterogeneity along transport pathways on the model output. We have included hetrogeneity as a property in the CRYSTAL3D model, which is used in Monte Carlo simulations of radionuclide transport. This model is as a submodel of a parallel Monte Carlo driver* . In Section 2, the role of probabilistic methods is considered in PA assessment. Section 3 briefly addresses the CRYSTAL3D model, and a case study is done in Section 4. Section 5 presents the results and Section 6 provides a summary of the main conclusions.
THE ROLE OF PROBABILISTIC METHODS IN PA ASSESSMENTS
Nuclide specific data like sorption, matrix diffusion data and solubilities, are typified by bands of uncertainty which tend to be large. As is also the case of properties like wet surface area, channel lengths and apertures, darcy velocities and longitudinal dispersion estimations. It is therefore common that, in parallel with deterministic transport model calculations, probabilistic calculations are done using Monte Carlo methods for the PA assessments. Evidently the reason for this, is to cover the spectrum of parameter uncertainties in a systematic way. There are also other types of uncertainties, such as those associated with the scenarios and the conceptual models which also motivate the use of Monte Carlo methods, but we disregard this aspect here as we are focusing on the issue of heterogeneity in PA assessments.
The transport models used in Monte Carlo assessments are, in general, 1D models that are relatively simple in comparison with the 2 and 3D hydrogeological models. This simplification is motivated by the fact that field data can be incomplete or inaccurate, or due to lack of knowledge, it might be meaningless to introduce detailed features in the codes when some of the data are ambiguous, or perhaps even not available. Another reason is that it can be prohibitive to run complex solute transport models because of the need to make many thousands of realizations in Monte Carlo assessments. The cost in terms of CPU-time, disk storage capacity and memory banks motivates keeping these models as simple as possible. The achievements of recent years in high-performance computer technology is reflected in the lower prices available nowadays and may imply an opening for the wider use of Monte Carlo methods incorporating more detailed models.
Heterogeneity, or expressing it in an alternative, but equivalent way, the averaging of properties along transport pathways is a feature that has not been fully appreciated up to now in Monte Carlo transport calculations.
THE CRYSTAL3D MODEL
The CRYSTAL3D model (1) has been developed to address the impact of heterogeneity on the consequences, as delivered by the Monte Carlo simulations of geosphere transport of HLW waste. This model is based on a simple extension, to 3D geometry, of the SKIs CRYSTAL model (2).
For the sake of completeness, we briefly describe the CRYSTAL code in this section. CRYSTAL is a 1D advective-dispersive transport model based on a pair of coupled partial differential equations (Eqs. 1 and 2). Basically, the first equation describes the transport of nuclides by water flowing in the fractures whilst the second one represents diffusion in the rock matrix. In conjunction with the transport equations, one uses the initial and boundary conditions which allow the specification of concentrations or fluxes. For details, the reader should consult Worgan et. al. (2).
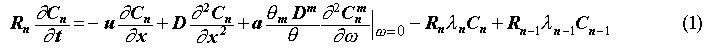
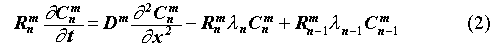
The subscript n denotes the nth radionuclide in the chain. Rn
[-] is the retardation due to linear equilibrium sorption on the fracture walls,
C(x,t) [moles/m3] the concentration of radio-nuclides in the
fracture pore water, t [y] the time, u [m/y] the velocity of water in the
fracture, x [m] the distance along the fracture, D [m2/y] the
longitudinal dispersion, Dm [m2/y] the matrix
diffusivity, 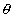 m the
matrix porosity,
m the
matrix porosity,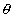 the rock
mass porosity, a [m-1] the specific wet area per volume of the rock
mass, Cm(x,w,t) [moles/m3] the concentration of
radionuclide in the static rock matrix pore water, w [m] the distance
perpendicular to the fracture and
the rock
mass porosity, a [m-1] the specific wet area per volume of the rock
mass, Cm(x,w,t) [moles/m3] the concentration of
radionuclide in the static rock matrix pore water, w [m] the distance
perpendicular to the fracture and
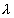 [y-1] the
radioactive decay constant. CRYSTAL has been used hitherto as a geosphere
transport submodel within the SYVAC/SU package for Monte Carlo assessments of
radionuclide transport. When CRYSTAL is used in a probabilistic fashion (more
than one realization), the input parameters that are allowed to vary, are
sampled from different probability density functions (pdfs). The code is run
thousands of times to obtain sufficiently high statistics for uncertainty and
sensitivity analyses to be done.
[y-1] the
radioactive decay constant. CRYSTAL has been used hitherto as a geosphere
transport submodel within the SYVAC/SU package for Monte Carlo assessments of
radionuclide transport. When CRYSTAL is used in a probabilistic fashion (more
than one realization), the input parameters that are allowed to vary, are
sampled from different probability density functions (pdfs). The code is run
thousands of times to obtain sufficiently high statistics for uncertainty and
sensitivity analyses to be done.
The transport length between the source and the biosphere is kept constant, i.e., it is the same for all realizations. This implies that the Monte Carlo simulations are performed for an "equivalent" fracture with the length being fixed for all the simulations.
In contrast to the concept described above, there is no "equivalent fracture" in the CRYSTAL3D model. In this model one defines a geosphere volume within which stochastic fractures are generated. Fractures connected in series, but having different lengths and orientations, form a pathway between the source and, for instance, a main fracture zone. The transport between this zone and the biosphere is assumed to be so fast that it can be considered instantaneous on a geological time scale. The parallel Monte Carlo driver samples the CRYSTAL3D input parameters, then calls CRYSTAL to simulate the transport in each of the fractures that constitute a pathway. The number of fractures vary from realization to realization because their length and orientation in space is also sampled. Typically for a distance equal to 500 meters between the canister and the fracture zone, CRYSTAL is called 100 times on average, once for each fracture of the pathway. And every fracture has its own geometrical and chemical properties. This procedure is repeated thousands of times in the Monte Carlo simulation, the number of times corresponding to the number of realizations specified by the code user. This is, in brief, the mechanism by which CRYSTAL3D introduces heterogeneity along the transport pathways.
Introducing this heterogeneity feature implies that we have increased the number of calculations by approximately two orders of magnitude over the Monte Carlo calculations that we have done before. Thus, we were forced to take advantage of high-performance computing, in our case by using an IBM-SP2 parallel supercomputer.
A CASE STUDY
To define a case study we make a certain number of assumptions that, for the sake of simplicity, we call a scenario. In our scenario we assume the existence of a single canister which for some reason fails, initiating a leaching process. Because we are interested in the impact of the heterogeneity in the far-field, we use the same source term for all realizations in the Monte Carlo simulation. The times series describing this source term is the same as that used in Andersson et. al. (1). The nuclide used in this study is 243Am, which has a half-life of 7.38 x 103 years. The far-field parameters used in CRYSTAL3D are summarized in Table I, together with the pdfs from which they are sampled and their respective ranges.
Table I Far-field Parameters Used in CRYSTAL3D. The Parameters are
Bound by the Cut-off Values
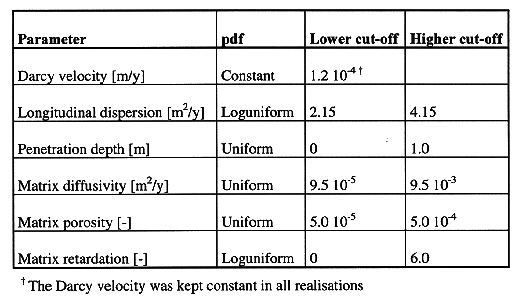
The reader should observe that, for reasons of mass conservation, the Darcy velocity for the different fractures forming a given pathway must be the same. This is so in CRYSTAL because the fracture aperture is constant. Obviously it is possible to vary the Darcy velocity from realization to realization, but it has been kept constant in our study.
RESULTS
In this work the sampling technique used to obtain the parameters was pure random Monte Carlo. The number of realizations was 5000. Each pathway had a mean of 110 fractures, which implies that the transport subroutine was called more than half million times. In applications done in the past, using the SYVAC/SU Monte Carlo driver (3,4), the number of realizations has been varied between 1000 to 2000, which is not generally sufficient. Having now introduced heterogeneity, the actual number of 5000 realizations is still too low for real production runs. Nevertheless the main conclusions presented here are valid and motivate the continuation of these studies with improved statistics.
The Actual Performance of the Parallel Monte Carlo Driver
A preliminary study of the elapsed time was done for 100 runs (10,000 calls to CRYSTAL). It is concluded that the parallel code performance is entering in the super-linear regime for 10 processors. In fact, Fig. 1 shows that the simulation using one processor takes 2196 seconds; thus for ten processors it should take 219.6 seconds in an ideal case. We obtained 253 seconds.
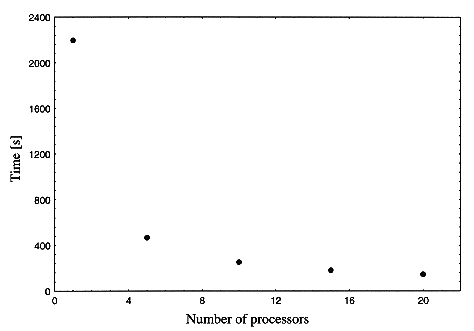
Fig. 1. Elapsed time versus number of
processors for 100 realizations.
Figure 2 shows that for ten processors, the elapsed time increases linearly with the number of realizations. For 5000 realizations it took 12,254 seconds with ten processors, i.e., the cost of communication between processors has decreased and the time elapsed is lower than expected(12,650 seconds). Thus the performance shown by Figure 2 has increased in going from 100 to 5000 realizations. This performance is in fact somewhat better than the one given by the linear extrapolation, which is considered "the ideal" case. We say therefore that the code is working in the super-linear regime.
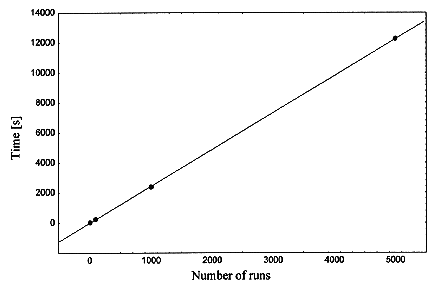
Fig. 2. Elapsed time versus number of
realizations for 10 processors
In conclusion, we can consider the actual performance of this first version of the parallel Monte Carlo driver as being very satisfactory, at least for 10 processors. Because of the nature of our problem we believe that it is not possible to go further into the super-linear regime.
The Results of Uncertainty Analysis
The Monte Carlo driver delivers 5000 breakthrough curves as the output of the simulation. The mean peak value is used as the risk measure (or consequence measure) in the analysis. The distribution of peak releases is shown in Fig. 3
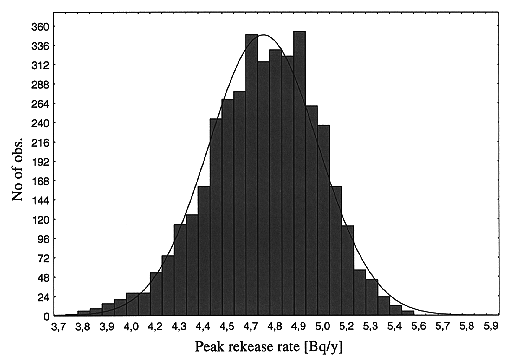
Fig. 3. Histogram of peak release
rate.
The distribution appears to exhibit a lognormal profile, but there is no theoretical foundation to justify this, so we do not use the equation fitted to the distribution to derive any summary statistics. Table II shows the mean and standard deviation of the peak at the 95% confidence level.
Table II Mean Value and Standard Deviation for the Peak Release
Rate of 243Am from 5000 Realizations Using CRYSTAL3D

The uncertainties associated with the output consequences, as a result of the propagation of parameter uncertainties through the CRYSTAL3D model, have two interesting characteristics as already shown in Ref. (1) : i) the peak distribution is significantly smaller than that usually obtained in Monte Carlo simulations without variability along the transport pathway and ii) the mean peak release is also smaller.
The impact of heterogeneity is easily explained. Suppose that a given pathway in one realization has 100 fractures and consider the case of varying only one parameter, for instance, the sorption coefficient Kd. We know that low Kd values imply high release rates. Obviously the chance of sampling Kd values for all 100 fractures of a transport pathway such that most of them fall in the tail of the distribution, which gives high consequences, is much lower than in the case of only having one "equivalent fracture" as the pathway, because in the latter case we only sample one Kd value. The same situation applies to the other parameters. Thus the number of pathways having "extreme" parameters that lead to peak releases in the low probability-high consequence tail of the output distribution is reduced significantly. An analogue argument can be applied for the low-consequence tail of the output distribution. Consequently, whenever heterogeneity along the pathway is considered in the transport calculation, the variance of the output distribution is reduced and the mean value of the peak releases decreases.
On Sensitivity Analysis of CRYSTAL3D: Results
In a sensitivity analysis (SA) one seeks the response to the following
question: what is the relative importance of the input variable
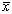 = (x1,...xi,...xp)
on the output variable Y = f(
= (x1,...xi,...xp)
on the output variable Y = f(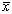 ),
where p is the number of parameters. Usually Y is a single value, but it can
also be a vector-valued quantity.
),
where p is the number of parameters. Usually Y is a single value, but it can
also be a vector-valued quantity.
The use of CRYSTAL3D leads to a new situation. The quantity Y = f(
 1,...
1,... i,...
i,... f), is now a function
formed of f vectors where f is the number of fractures for each pathway and
f), is now a function
formed of f vectors where f is the number of fractures for each pathway and
 i = (Wi1,...Wii,...Wip)
a vector consisting of p input parameters. This situation raises a new challenge
to global sensitivity analysis. The SA methods used hitherto, like Spearman
correlation coefficients, Partial Rank Correlation Coefficients (PRCC), Sobol
sensitivity indices, FAST (Fourier Amplitude Sensitivity Technique) do not seem
to cope with this situation directly, other than by reducing the "dimensionality"
of the problem.
i = (Wi1,...Wii,...Wip)
a vector consisting of p input parameters. This situation raises a new challenge
to global sensitivity analysis. The SA methods used hitherto, like Spearman
correlation coefficients, Partial Rank Correlation Coefficients (PRCC), Sobol
sensitivity indices, FAST (Fourier Amplitude Sensitivity Technique) do not seem
to cope with this situation directly, other than by reducing the "dimensionality"
of the problem.
In this paper we have applied the technique of reducing the dimensionality of the problem before using PCR (Partial Correlation Coefficients). By reducing the dimensionality of the problem, we mean simply that we take single parameter values for each pathway by computing, for instance, the mean value or median of these parameters. Once we have obtained them, we have reduced the problem to the traditional one and therefore we are in position to apply the usual SA techniques.
In our analysis we have used the median of the parameters for each pathway. The results obtained are show in Table III.
Table III The Impact of the Variable Geosphere Parameters on the
Peak Release Rate
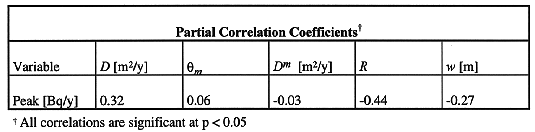
Table III shows that the retardation coefficient is the most important parameter followed by longitudinal dispersion and penetration depth. The remaining parameters can be considered of no relevance.
The importance that the parameters have for the consequences is, in decreasing order of magnitude:
Retard. coef. > Long. disp. > Penet. depth > Matrix porosity > Matrix diffusivity.
The retardation coefficient and the penetration depth have negative correlation values. Thus, the lower these coefficients are, the higher will be the peak release rates. On the other hand the positive value of the correlation associated with the longitudinal dispersion imply that high dispersion is associated with high peak release rate.
The reader should recall that the groundwater flow rate has been kept constant, but it is well known that it is the most important parameter. By keeping it constant, we have been able to enhance the relative sensitivity of the other parameters, thereby avoiding the need to use rank correlations in the sensitivity analysis.
Figure 4 presents the scatter plots of peak release versus two variable parameters which illustrate the subjacent correlations between parameters and the output consequences. The ellipses represent the 95% confidence level boundaries. As expected from the results of Table III, the scatter plot of the retardation coefficient of Figure 4a illustrates a stronger correlation with the peak release rate than the scatter plot of the penetration depth which is the third parameter in importance.
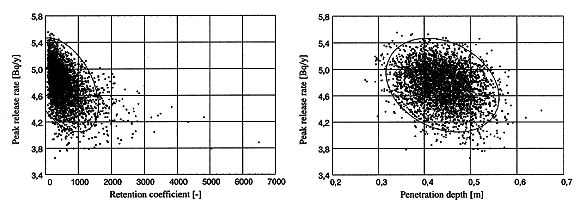
Fig. 4. Scatter plots showing peak
release versus retention coefficient (left) and penetration depth (right).
SUMMARY
The CRYSTAL3D model has been used as a submodel of a parallel Monte Carlo driver to do a variability study of geosphere parameters. The aim was to evaluate the impact of heterogeneity on the output consequences delivered by the model.
In the first study of this issue, referred to previously and to be published elsewhere, we varied two parameters and used 1000 realizations. In this study we have increased the number of parameters to five and the number of realizations to 5000, which resulted in half a million calls to the transport subroutine.
The present results confirm the indications of our first study referred in the above paragraph, that the variance of the output distribution decreases, as well as the mean peak release. It also points out that avoiding a more realistic treatment of fracture media heterogeneity, can result in estimations, from probabilistic assessments, that are too conservative, at least for the traditional models using the 1D advective-dispersive transport equations.
A systematic study using several nuclides, realistic data and a higher number of realizations is necessary to obtain more reliable statistics on the effects of the heterogeneity of fractured media.
REFERENCES
ACKNOWLEDGMENTS
The authors thank the Swedish Nuclear Power Inspectorate (SKI), the European Commission and the Parallel Computer Centre (PDC) for their support. The Swedish Nuclear Power Inspectorate is supporting our work in the field of PA assessments of radioactive waste. The development of the parallel Monte Carlo driver is also being made possible by the support of the European Commission under contract F14W-CT95-0017 (GESAMAC project) within the frame of the R&D programme: "Nuclear Fission Safety" (1994-1998). The Parallel Computer Centre has kindly put the IBM SP-2 facility at our disposal for the present work.
* The actual M.C. driver form the skeleton of the parallel PREP M.C. driver being developed for the European Union GESAMAC project.