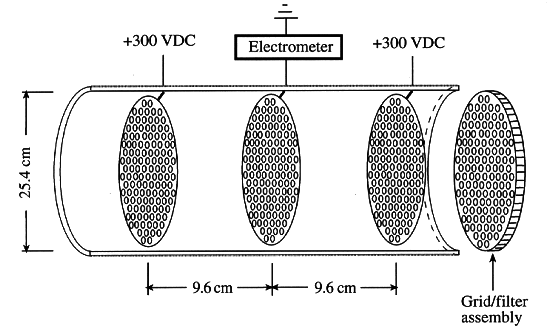
Fig. 1. Cutaway view of one of the
detector volumes. Not shown is a grid/filter assembly, identical to the one in
the figure, that is situated on the left-hand side of the detector assembly.
C. R. Whitley, P. A. Steadman, D. W. MacArthur, J. G. Conaway
Los Alamos National Laboratory
ABSTRACT
This paper describes a radon monitor developed at the Los Alamos National Laboratory for analyzing stack emissions from the Fernald Vitrification Facility pilot plant now under construction. During the vitrification process, radon offgas is expected to be released into the atmosphere even though radon scrubbing systems will be used. To operate the plant in the most economical way, it is desirable to have a reliable radon monitor that would prevent the occurrence of unnecessary and costly shutdowns. The monitor described here incorporates long-range alpha detection (LRAD) technology. Its intended purposes are to supplement other radon monitoring systems at Fernald and to demonstrate the sensitivity and reliability of this new type of monitor.
The monitor is to receive a continuous, HEAP-filtered, isokinetic sample of stack emissions. With LRAD technology, ions created in the detector volume by energy loss mechanisms of decay alphas are collected on a charged plate, and the current generated by this is measured with a sensitive electrometer. In electrostatic LRAD designs, the linearity of the measured current with gross alpha activity is well-established. To address the potential presence of thoron (220Rn) in the emissions, a double-chambered monitor was designed to discriminate between thoron and the radon isotope of interest (222Rn). This method relies on a continuous flow of the sample through the detector, with a length of pipe between the two detection chambers providing a time delay that allows substantial decay of the relatively short-lived thoron. A computer code then unfolds the amount of 222Rn present in the stack. In addition, the code accounts for plating of the charged daughter products from both isotopes on the interior surfaces of the detector, which themselves can contribute greatly to the gross alpha activities. The algorithm has been shown to be stable and self-correcting in laboratory studies.
Calculations and the results of tests and preliminary calibrations show this monitor can detect the presence of 222Rn in concentrations from 20 pCi/l to nearly 100,000 pCi/l. The tests indicate the monitor can achieve the design goal of detecting concentrations as great as 200,00 pCi/l, and have a minimum sensitivity of 10% throughout its range using a five minute integration time. The monitor should provide a rugged, reliable, and sensitive radon detection system requiring little maintenance.
INTRODUCTION
The stack monitor uses long-range alpha detection (LRAD) technology for the measurement of radon levels in stack emissions. The basic principle behind LRAD is the collection of ions created in air through the energy loss mechanisms of decay alphas (1). This is accomplished by establishing an electric field in the region where alpha decays will occur, and directing the ions via the field onto a biased plate. Accumulation of charge on the plate results in a current in the biasing circuit which can be read with a sensitive electrometer. In electrostatic LRAD designs, the linearity of the measured current with gross alpha activity is well-established.
The monitor was designed to have two gross-alpha detection chambers with a delay chamber between them. Knowledge of the flow rate of a continuous HEAP-filtered stack sample through the monitor allows discrimination between radon-222 (hereafter referred to as radon) and radon-220 (hereafter referred to as thoron), when preprocessing of the emissions allows decay of other, much shorter-lived radon isotopes.
Figure 1 shows a detail of one of the detectors. Filter assemblies on either side of the detector volume are intended to provide a uniform airflow through the detector. The actual velocity profile of the airflow within the volume is of lesser importance than insuring that the airflow is identical in the two detectors. Three grids between the filters are used to collect ionized particles. Each grid is a circular stainless steel plate, 0.15 cm thick, and perforated with 0.32 cm-diameter holes to give 40% open area in the plates. The grids extend to nearly the inner diameter of the pipe, where they are suspended from the inner walls with Lexan standoffs. The two outer grids, each 10.2 cm from the center grid, are placed at +300 VDC, while the inner grid is connected to ground through a Keithley 6517 electrometer.

Fig. 1. Cutaway view of one of the
detector volumes. Not shown is a grid/filter assembly, identical to the one in
the figure, that is situated on the left-hand side of the detector assembly.
When radon or thoron enter the spaces between the grids, the electric fields direct negative ions created from alpha decays onto the positive-biased grids. Positive ions are directed both onto the grid at ground (signal grid) and the walls of the detector.
When an atom of radon undergoes alpha decay, the daughter is generally left with a net positive charge and will also be deposited on either the detector wall or the signal grid. Over time, this effect results in the accumulation of radon daughters within the detector volume that contribute to the observed alpha activity. For instance, radon has in its decay chain Po-218 and Po-214, each of which decays by alpha emission. By determining the contribution to the signal of these daughters, their effects can be accounted for and subtracted from the total signal.
The operation of the monitor is controlled by computer code. When executed, the code performs all necessary initialization of the electrometer over an RS-232 line, reads the current in the two detectors in sequence, and then performs calculations using these signals to extract the radon and thoron concentrations present in the first detector. The results are printed to a computer monitor screen and written to files.
THEORY OF OPERATION
The signals from the two detectors are considered to be due to external background sources, radon, thoron, and their radioactive progeny. Background signals over several days show only small variation with time and can thus be treated as constants. The decay of radon and thoron produce immediate contributions to the signal as well as delayed contributions from subsequent decays of their plated daughters. Because of the different decay alpha energies of the various isotopes involved, radon and thoron must be treated somewhat differently when calculating their concentrations in the sample. The calibration for radon and thoron also differ because of the decay of thoron within each detector. At a nominal flow of 1 liter/sec, thoron that enters detector 1 requires about 10 seconds to traverse its 20.3 cm length. The thoron concentration at the exit is then only about 90% of that at the entrance.
Radon decays by emitting a 5.49 MeV alpha particle, while a thoron decay produces a 6.29-MeV alpha, followed almost immediately by a 6.78-MeV alpha from the decay of the daughter Po-216. Thus the signal from a given amount of radon activity will yield a lower signal than the same amount of thoron activity. The ratio of the signals is not simply the ratio of the alpha energies, due to the geometry of the detector and the effective collection region. However, using sources that produce known activities per time of radon and thoron, the constants relating activity/volume to signal from the detector can be determined. A signal from radon or thoron will be a linear function of its concentration, and hence of the number of decays that occur. It follows that the number of daughters plating per unit time within the detector is proportional to the signals from radon isotopes. Once known, the proportionality factor allows for computational "tracking" of the background signals due to the daughters.
The process of data acquisition and computer analysis can be summarized by the following sequence of events which are controlled by computer code:
- Electrometer reads current first in detector 1 and then in detector 2.
- Background contributions from daughters plated within the detectors are subtracted from these readings to obtain signals due to radon/thoron.
- Radon/thoron signals are converted to units of pCi/l and printed to screen and saved to file along with local time information.
- New background levels are calculated from deduced radon/thoron levels.
- Repeat (1)-(4).
Noting first that the long half-life of radon (3.8 days) results in no sensible loss of radon concentration between the two identical detectors, we have equal contributions to both signals from radon and its plated daughters. Any difference between the two signals will be due to thoron decay. The thoron will decay to Po-216, which has a half-life of 0.16 seconds. This isotope also decays by alpha emission to Pb-212, which plates out within the detector. The eventual decay of Pb-212 to the stable Pb-208 produces in its decay chain one alpha. With this information, we let
Sig 1 = raw signal from detector 1,
Sig 2 = raw signal from detector 2,= inverse mean life of thoron,
t= transit time from detector 1 to detector 2,
Rad 1 = Rad 2 = radon contributions to signals,
RadBack 1 = RadBack 2 = radon daughter contributions to signals,
Thor 1(2) = thoron contribution to detector 1(2), and
ThorBack 1(2) = thoron daughter contributions to detector 1(2).
Here, Sig1 and Sig 2 are the results of subtracting external backgrounds from the raw signals, and applying a normalization factor to account for any asymmetry between the overall collection efficiencies of the two detectors. The thoron and thoron daughter contributions are related by
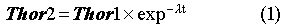
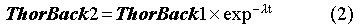
Since
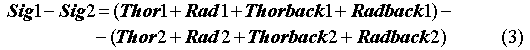
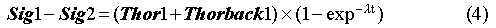
The transit time t used here is the effective time for thoron to pass from detector 1 to detector 2. The average linear speed uav of the flow is equal to (volume flow)/(cross- sectional area), so at a volume flow of 1 liter/sec, uav is about 2 cm/sec. With this geometry, the airflow between the detectors approaches a parabolic velocity profile as it nears detector 2 with a maximum speed along the axis of nearly twice the average airspeed. Much of the mass flow occurs, then, at speeds greater than the average and experiences less decay. Although some of the mass flow occurs at less than average airspeed, the net result is that the amount of decay seen at detector 2 is less than would be assumed using only the average airspeed so that t < tav.
While the effective transit time is best found by using a thoron source and observing the amount of decay seen between the detectors, a good approximation can be calculated from the equations for the radial velocity u(r) (4)
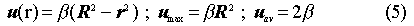
where R is the inner radius of the pipe. These equations hold for airflow in circular pipes in which the final state velocity profile has been achieved (Poiseuille flow). Although the final state profile is only asymptotically reached, the expected airflow though the monitor has a Reynolds number of ~200 so that after several feet beyond detector 1, the velocity profile is already approximating the final state. The results of a computer code written to add contributions from different radii in the pipe, each of which experiences decay based on the airspeed at that radius, show that an average airspeed of 2 cm/sec results in an effective airspeed of 2.5 cm/sec, in good agreement with thoron measurements at a volume flow of 1 liter/sec.
By knowing the initial backgrounds in the detectors from radon and thoron, the computer code can extrapolate the background at later times so that we can calculate the radon and thoron concentrations in the first detector using the relations
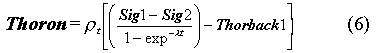
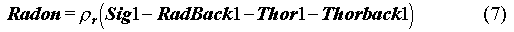
Here, 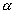 t and
t and
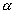 r are factors that relate the raw
signal contributions of the radon and thoron to activities in pCi/l. In
addition, the factor
r are factors that relate the raw
signal contributions of the radon and thoron to activities in pCi/l. In
addition, the factor 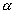 t accounts
for the immediate decay of the thoron daughter Po-216.
t accounts
for the immediate decay of the thoron daughter Po-216.
We can break up the 's into their constituent parts as follows:
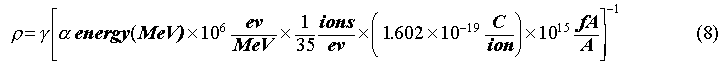
which reduces to
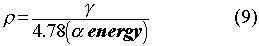
with 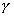 in pCi/dps. The
determination of the
in pCi/dps. The
determination of the 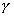 's for
radon and thoron is part of the calibration of the monitor, and is accomplished
by using known concentrations to produce a signal in the detectors.
's for
radon and thoron is part of the calibration of the monitor, and is accomplished
by using known concentrations to produce a signal in the detectors.
To find the daughter background contribution to the signals, we first derive
a number N for the number of radon or thoron atoms in the detector by
calculating the activity in dps (e.g., thoron activity =thoron/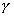 ), so that
), so that
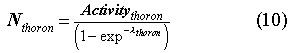
where  is in inverse
seconds.
is in inverse
seconds.
There are two incremental contributions in the calculation of the number of daughter atoms of a given isotope: an increase from the decay of the parent and a decrease from decay of the daughter atoms already present. Assuming a constant concentration of the parent species, the increase in the number of atoms N is governed by the relation
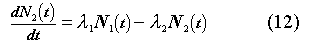
where the subscripts 1 and 2 refer to the parent and daughter species,
respectively, and the  's
are inverse mean-lives. The daughter decay causes a loss of already present
atoms at a rate
's
are inverse mean-lives. The daughter decay causes a loss of already present
atoms at a rate
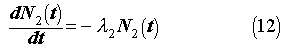
From these contributions we can calculate the number of daughters at time t+![]() t
as
t
as
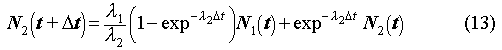
The activity A of the daughter in disintegrations per second is
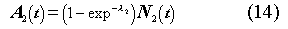
where 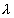 2 is
in inverse seconds. The signal S from the daughters is then
2 is
in inverse seconds. The signal S from the daughters is then
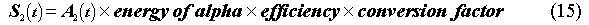
The conversion factor is a numerical constant to give S in units of fA.
When the parents are radon or thoron, their number N1(t) need not be known absolutely--it is sufficient to assign a number proportional to the signal they produce. A subsequent efficiency factor accounts for the uncertainty of the actual number. The efficiency factor is a function of alpha energy, and so must also account for effects due to the path lengths of decay alphas. The positively charged daughters of radon and thoron are deposited both on the signal grid and on the walls of the detector. Many of the alphas emitted from the plated daughters on the signal grid will not lose all of their energy in the effective collection volume of the detector, while some alphas from daughters plated on the detector walls will lose some of their energy there. It can be seen from the shape of the effective collection region that an increase in alpha energy from sources plated on the signal grid will have relatively mild effects on the amount of ionization collected, while for sources plated on the detector walls an increase in alpha energy will allow substantially greater penetration into the effective collection region. These effects are difficult to calculate accurately but can be measured by fitting the decay curves of the plated daughters after the detector signal has achieved equilibrium with a source of radon or thoron. This procedure gives relative efficiency factors for the plated daughters.
After reading the current from detector 1 and detector 2, the computer code updates the new values for the number of relevant decay products inside the detectors using the formula
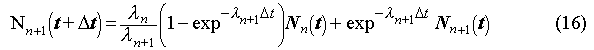
and then their signal contributions Sn+1, as before. The individual contributions from the radon and thoron daughters in each detector are then summed to give the plated daughter background signals in each detector. This process is repeated at intervals of length Dt, which is the interval of time required for the scanning electrometer to obtain a current measurement from both detectors.
TEST RESULTS
Testing of the monitor was limited by the availability of radon and thoron sources. Most results were obtained using thorium ore specimens which supplied approximately 500 pCi/sec of thoron. At the airflows used (generally near 1 liter/sec) the concentration was about 500 pCi/l. In long test runs in several prototype monitors, both airflow and electrostatic, the source showed diurnal fluctuations in thoron output which were attributed to temperature fluctuations.
Figure 2a shows a run in which there are initially only background levels of radon present. A regulated compressed air supply created the airflow through the monitor. The thoron source was then placed in a pipe just upstream of a HEAP filter so that the monitor would see only background ionization and that due to thoron and its progeny. The figure shows the immediate rise in signal of the first detector, followed closely by a lesser rise in the signal of detector 2. The slow initial decrease in both signals is attributed to a decrease in the thoron output of the source. The decrease is reflected in the calculated thoron and radon levels shown in Figure 2b. The statistical error in the calculations, using the 2.5-minute effective time averaging in the code, is <5% for concentrations as low as 200 pCi/l. The small spikes seen at the point of insertion of the thoron source is due to the invasive nature of the method of insertion, which required temporary disruption of the airflow.
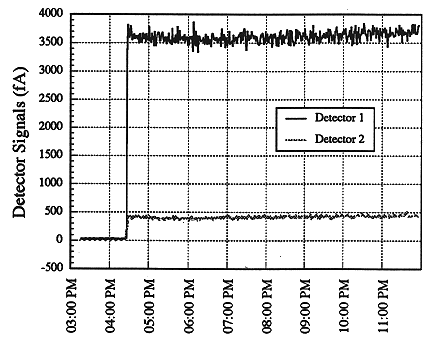
Fig. 2a. Signals in the two
detectors from a thoron source. At around 5:00 PM the source is placed in the
airstream.
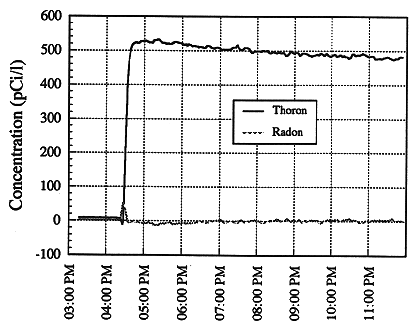
Fig. 2b. Concentrations of radon and
thoron calculated from the data of Fig. 2b.
The relative contributions from the daughter Bi-212 (33% decay via a 6.07 MeV alpha to Tl-208 and 67% decay to Po-212, which decays immediately via a 8.78 MeV alpha to Pb-208) were determined from fitting the decay curve of a run of sufficient length for the thoron daughters to reach equilibrium. By subtracting the signals obtained immediately after the source is removed from the signals just before its removal, we get the signal due to the thoron source alone. The ratio of the pure background signal to the pure thoron signal gives the factor relating their relative contributions. In the code, this factor is modified by the alpha energies of the decay products.
A similar procedure was performed using the available radon source, which was a specimen of natural uranium ore. The specimen was found to emit approximately 4 pCi/sec of Rn-222. Natural uranium contains only small amounts of U-235, from which Rn-219 is derived, but it produces a considerably greater activity of Rn-219 than Rn-222 because of its short (~4 seconds) half-life. To eliminate the Rn-219, a long (~2 minutes) delay line was placed between the source and a prototype detector, and the airflow from the compressed air source was adjusted using a regulator. By reducing the flow, a much larger concentration of Rn-222 was able to be examined. The daughters of radon are fairly short-lived (<30 minute half-lives) so equilibrium could be achieved after only a few hours.
The factor for the thoron daughter Bi-212 was found to be 0.55. This factor multiplies the weighted average energy of 7.87 MeV of the two alpha decay pathways mentioned earlier. Fitting the decay curve of the radon daughters gave the factors 0.405 for Po-218 and 0.515 for Po-214. These factors also multiply the respective alpha energies of the respective isotopes to yield their signal contributions as they plate out within the detectors.
The relative strength factors for the daughters and the conversion factors for radon/thoron signals to radon/thoron concentrations will be differ from these when the atmospheric pressure at which the monitor operates is changed substantially. At Los Alamos, New Mexico, where these measurements were taken, the pressure is around 11.5 psi. Near sea level, atmospheric pressure is near 15 psi, and alphas of a given energy will have a shorter range there. As described before, the geometry of the detectors and the field lines generated within them alter the efficiencies of ion collection by the detector grid in a manner dependent on the alpha range. It is necessary in any case to calibrate the monitor with known sources, and the relative strength factors for the daughters can be extracted from the same data.
The algorithm for the computer code has been tested for stability using simulated data. The data was generated at the same time intervals as that produced by the actual monitor and a Guassian error is introduced of the same magnitude as observed in actual data. When using the code to determine the radon and thoron concentrations from the simulated data, scenarios were created by supplying the code with inaccurate initial or operating conditions. One situation of interest is when significant background signals due to daughter plating are present in the detectors, while the code is initiated with background levels equal to 0. In simulating this scenario, the airflow was set to be 1 liter/sec with 20,000 pCi/l of radon and 10,000 pCi/l of thoron, and the code was allowed to generate four days of data. The radon and thoron concentrations were chosen to reflect maximum estimates of their possible activity ratios. Figure 3a shows the simulated data over the fourth day when background contributions had reached equilibrium with the radon and thoron levels. The data shown is time averaged over one minute intervals. Figure 3b shows the results of running the code with the data of the fourth day as input. After two hours, the code converges to the correct value for the radon concentration. The thoron concentration takes longer to approach the correct value. The times for the calculated radon and thoron concentrations to reach the correct values in this simulation are closely related to the dominant half-lives of their respective decay products; i.e., the 27-minute half-life of Pb-214 for radon, and the ~11-hour half-life of Pb-212 for thoron.
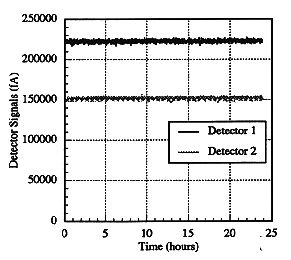
Fig. 3a. Simulated data assuming
initial radon concentration of 20,000 pCi/l and 10,000 pCi/l of thoron at 1
liter/sec. Data shown in fourth day of run, where radon/thoron daughter activity
has reached equilibrium with activities of these concentrations.
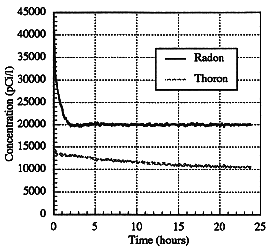
Fig. 3b. Results of running code
using the data of Fig. 10. Initial conditions are assumed to be an airflow of 1
liter/sec and no signal due to daughter plating. The code converges on the true
value for radon within a few hours. True thoron levels are asympototically
reached with a half-life of ~11 hours.
Another simulation created data with the same radon and thoron concentrations as before, starting with no background plating present. The airflow was initially set to be 1 liter/sec, but then was given a sine wave variation in time with a two-hour period, imposing a ±10% variation in the average airspeed. The one minute time-averaged data over a one day period is shown in Figure 4a. Detector 2 had fluctuations due to the varying decay time available to the thoron. Figure 4b shows the results of running the code to unfold the radon and thoron concentrations while assuming a constant airflow of 1 liter/sec. Both concentrations have a ±5% variation around their correct values as a consequence of assuming a constant airflow existed. The variations would decrease in magnitude as the relative concentration of thoron was decreased.
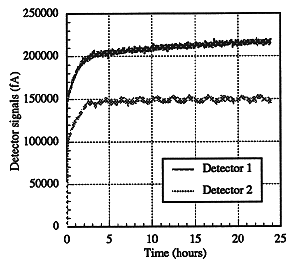
Fig. 4a. Simulated data assuming
radon/thoron concentrations as before, with a 10% sine wave variation in the 1
liter/sec airspeed.
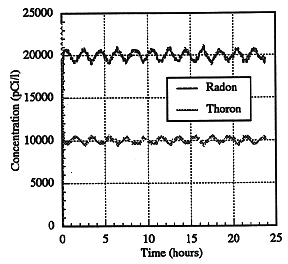
Fig. 4b. Code analysis of the data
of Fig. 12 shows ~5% variation around the true radon/thoron values. The
magnitude of the variations is tied to the actual thoron levels.
CONCLUSIONS
A stack monitor capable of discriminating between 222-Rn and 220-Rn over a wide range of concentrations has been developed at Los Alamos National Laboratory. With proper calibration the levels of these two isotopes can be determined to within about 5% at levels of 20-100,000 pCi/liter. Tests and simulations show it to be a stable system that could operate with minimal maintenance over long periods of time, and due to the simplicity of its design, it is both rugged and inexpensive to maintain.
REFERENCES
CONTACT
For further information on LRAD technologies, contact
James E. Koster
Project Leader
Environmental Applications, NIS-6
Mailstop J-561, Los Alamos National Laboratory
Los Alamos, NM 87545
(505) 667-3346 / jkoster@lanl.gov