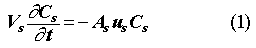
Erik Vold
Los Alamos National Laboratory
Rob Shuman
Rogers and Associates Engineering Corporation
ABSTRACT
Analytic and numerical modeling of the aqueous phase release to the unsaturated zone of low level radioactive waste from a shallow burial disposal facility was initiated last year (Phase One) for the Los Alamos Area G Performance Assessment. This year (Phase Two) the effort is continuing to refine the results in the previous analyses. The previous results showed that the 'rapid release' waste category (with solid-liquid phase partition coefficient, Kd = 0) dominates the peak release concentrations and therefore controls the offsite dose. The model for the dissolution transition from the waste package solid phase to liquid phase for the rapid release inventory is improved to reflect a transition limited by the local percolation rate. The analytic solution to the previous model was singular for this case, and so a new solution is derived and applied to the site assessment. A detailed numerical analysis is completed of transient percolation and its effect on the source release model output as a function of time. Transients can be significant locally but attain average values rapidly over local variations in time and space. The site inventory is sorted into groups by time period of interest, allowing analysis of nuclide solubility limits by individual disposal unit. A detailed implementation of the source release model has been incorporated directly into the source term module of the 3-D unsaturated zone computational model used in the site performance assessment.
INTRODUCTION
A Performance Assessment (PA), as required by DOE orders, is underway for the Low Level Radioactive Waste (LLRW) disposal facility at Los Alamos National Laboratory, Area G (1). This assessment provides the technical basis for disposal operations and for establishing environmental compatibility of those operations. Fig. 1A shows a cross-section of the mesa-top disposal facility at Area G with three representative disposal units.
A model for the aqueous phase release of low level contaminants to the unsaturated zone by a prescribed percolation rate and the subsequent leaching of contaminants has been explored in the preliminary PA (1) with the model development described previously (2) and its application to the preliminary site PA in (3). This report summarizes results from the previous analyses and describes model improvements and the continuing effort to refine the results in several areas. These include a refined percolation model for the dominant 'rapid release' wastecategory, an examination of the effects of percolation transients on source release, and a methodology to apply the analytic model results to specific disposal units across the site.
Synopsis of Preliminary Source Release Model
The conceptual model for subsurface liquid phase release from a disposal unit is shown in Fig. 1B. A representative waste package is shown to the left, and a disposal unit is shown on the right. Waste packages for a given nuclide and for a given package type are distributed more or less randomly throughout the disposal unit volume and thus the leachate through the waste packages approximates a uniform volumetric source term to the disposal unit volume. In the model, contaminant moves through three compartments (Fig. 1C) from the waste package solid phase to the waste package liquid phase by a dissolution process, from the waste package liquid phase to the disposal unit by percolation leaching, and finally from the disposal unit to the unsaturated zone by percolation. Analytic solutions were derived for the three compartments (2). It is critical to distinguish the waste package solid and liquid phase compartments because the maximum contaminant leachate concentrations occur within the waste package leachate. Therefore, the elemental solubility limit must be applied to the concentrations at that point as detailed previously (2), before dilution occurs throughout the disposal unit volume.
In application to the site Performance Assessment, the solution for the efflux from the waste package liquid phase (compartment 2) has been used directly in the numerical transport model for the unsaturated zone (4), with the waste leachate source term distributed over the computational grid points which represent the disposal unit volumes. Thus, the focus here is on the concentration and efflux solutions from the second compartment in the model. The governing equations of interest are derived as the contaminant mass continuity equation in the control volume or integral form for each model compartment. The result for the first compartment, the waste package solid phase, is
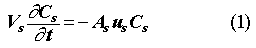
and for compartment 2, the waste package liquid phase,
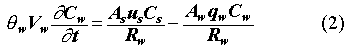
where subscript s refers to the waste package solid phase, and w refers to
waste package liquid (water) phase. C is the contaminant concentration, us is a
specified dissolution velocity, R is the standard retardation coefficient, R =
(1. + K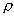
m/
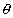), and is the moisture content
volumetric fraction, q is a Darcy flux (flux of liquid volume), V is a waste
volume from the data base, and A is an area in the horizontal plane. The waste
packages have an average height dimension (hw) taken to be 1m, and A = hw/V.
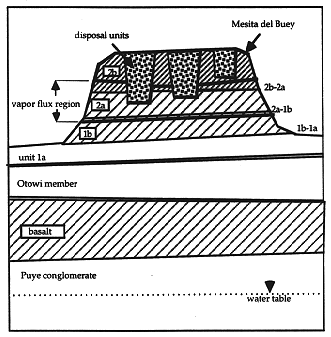
Fig. 1A Sketch of the stratigraphy
cross-section underlying the disposal facilities at Area G. The figure
dimensions are not to scale; the mesa top to canyon floor distance averages
about 100 ft, the canyon floor to the water table is about 800 ft, the mesa
width varies from 400 to 1200 ft. The cross-hatched regions indicate the more
fractured stratigraphic units. The 'vapor flux region' is discussed in the text.
Fig. 1B. Conceptual model for
subsurface liquid phase release from a disposal unit. A representative waste
package (solid phase, s and liquid or water phase, w) is shown to the left, and
a disposal unit (d) containing many randomly distributed waste packages is shown
on the right.
Fig. 1C. The three compartments in
the present release model are an equivalent representation of the conceptual
model from Fig. 1a, showing contaminant concentrations, C, and flux,
for the three compartments.
The analytic solution to Eqs.1 and 2 with initial conditions, Cs set to the data base inventory concentration, Cso, and Cw = 0., was given (2) as,
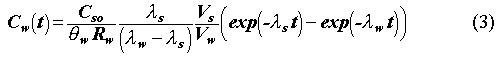
with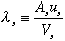 
and
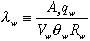
The moisture content, ,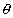
and percolation rate, q, through the waste are assumed the same as through the
disposal unit, with 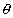= 0.08
determined from empirical data (5) and q ~ 5 mm/yr determined from modeling (6)
and analytic sources summarized in a companion paper (7). Waste and disposal
unit dimensions and volume are from the site data base, and to simplify, it is
assumed that As = Aw and Vs = Vw
.
Synopsis of Preliminary Model Results
The data base for disposed radionuclides at Area G allows inventory to be sorted by nuclide, by disposal package type (>50 waste package types are identified as related to different process streams), and by disposal unit (DU) location (over 30 disposal pits and 100 disposal shafts covering a 60 acre site). The data base must be simplified with justified approximations in order to simplify the source term to a manageable calculation even in a computerized analysis. Performance assessment pathway analysis requires that nuclides be distinguished, so the tradeoff for simplification is between waste package forms and waste disposal location. Phase One analysis simplified disposal location while tracking waste forms in detail. Phase Two analysis simplifies waste form as justified in this discussion, and tracks disposal location in detail for input to the 2-D and 3-D unsaturated zone transport model (8).
The preliminary PA analysis (Phase One) focused on a simplification over disposal units where inventory was averaged over those disposal units utilized in the 'historical inventory' (1988-1995). This allowed a detailed sorting and analysis by waste form where the >50 waste codes were approximated by four 'release categories' characterized with distinct parameter values in the source release model. A 'rapid release' category includes the waste inventory where the data base did not have specific enough data to justify any retardation or retention for the waste package form, and so Kd= 0, or Rw = 1 applies to this waste category, and the 'rapid release' waste is assumed to be leached as soon as water percolates through the closed disposal unit.
The previous analysis demonstrated clearly that only the inventory in the 'rapid release' category is significant in predicting maximum leachate concentrations and thus we need consider only the 'rapid release inventory' to predict the maximum drinking water dose or all pathways dose that eventually occurs after contaminant migration from the site. The specific criteria for comparing release concentrations based on inventory sources across different waste forms is Qij/Rij where i is the nuclide index, j is the waste form or category index, and Q is the inventory quantity per DU. This was examined in the data base across the entire inventory and the 'rapid release inventory' was confirmed to dominate for all nuclides. For Am-241, even though much of the inventory is in the sludge/concrete waste category, R ~ 5000 applies to that waste form (9) and so that waste release category does not contribute to maximum release concentrations. A few nuclide elements including uranium were consistently solubility limited and for these cases, the contributions across waste categories were calculated separately in the site assessment.
This allows us in Phase Two to use only waste inventory in the 'rapid release' category. This justified simplification allows us to evaluate the rapid release inventory by each disposal unit throughout the mesa top 60 acre Area G site. This provides detailed input to the 3-D unsaturated-saturated transport numerical study.
ANALYSES
Percolation Limited 'Rapid Release'
The characteristic time for waste package inventory to be available for
dissolution in the liquid phase of the water percolating through the waste
packages within the disposal unit was previously set as a constant based on
waste form and empirical data where available. Unfortunately, no data is
available for the release from the rapid release category under in-situ
conditions at Area G, so it was assumed to be 'rapid' relative to the
percolation transit time through the waste package, Tw = (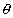whw)/qw.
Under the conditions now assumed for 'rapid release' waste, the transition
from the solid to liqud phase by dissolution will be limited by the moisture
percolating into the waste package. Thus, this transition is controlled by the
same percolation rate which controls the leachate release from the waste package
and so the same characteristic time constant applies to the release from
compartment 1 or 2. In Eq. 1 and 2, Rw = 1, and us = qw/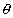 and so
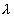s =
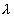w, and
therefore the analytic solution in Eq. 3 becomes singular.
For this singular case, the solution to Eq. 1 and 2, is rederived for
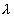s =
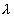w =
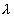= 1/Tw = qw/(hw 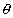w), and assuming Vs=
Vw. The analytic solution for this case, where the solid to liquid
phase dissolution process is limited by the moisture percolation into the
package and the leaching from the package is controlled by the same percolation
rate, becomes
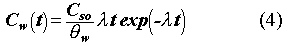
It is easily shown that the maximum concentration in the waste package
liquid phase, Cw-max, is given as Cso/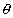we, where e is the
natural log constant or, Cw-max ~ 0.37Cso/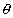w. The time this
maximum occurs is t = Tw = 1/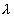 . The time dependent leachate efflux
from the waste,
w(t),
is
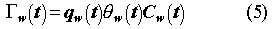
For the analytic solution, Cw(t) is given by Eq. 4, and the Darcy flux and moisture contents are approximated as constant values from appropriate time averages.
The result of varying a fixed dissolution time constant, Ts = 1/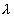s, from Eq. 3 is compared
to the singular case solution (T = Ts = Tw) from Eq. 4,
in Fig. 2. The figure shows a normalized concentration, Cw/(Cso/w), in waste leachate
water verses time for the 'rapid release' waste category, using several values
for T, the transition time from the solid to the liquid phase within the waste.
The limit as T goes to zero corresponds to a simple release model where the
contaminant concentration is instantaneously mixed into the moisture volume
fraction (and thus concentrated), and subsequently decays in time through
percolation from the waste package. The singular solution to Eq. 3 occurs for T
= 16 years. This case is used in the site performance studies and assumes the
dissolution transition is limited by the percolation through the waste package.
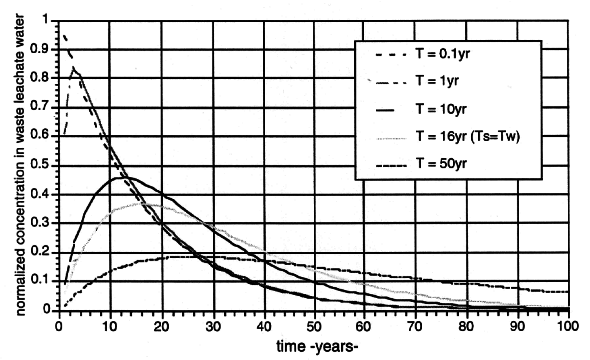
Fig. 2 Normalized concentration in
waste leachate water for the 'rapid release' waste category, using several
values for T = Ts, the transition time from the solid to the liquid
phase within the waste. The case (T = Ts = Tw) is used
in the site performance studies and assumes the transition is limited by the
percolation through the waste package. Concentrations are normalized to initial
solid phase waste concentration per moisture content, Cso/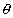w.
Transients in Percolation
The source release model includes a set of governing equations and the
analytic solutions which apply under simplifying assumptions such as a constant
percolation rate. Numerical solutions to the governing equations were obtained
for transient percolation rates to evaluate the validity of this assumption.
Results for the transient case are found by numerically integrating the
governing equations, Eq. 1 and 2, to obtain Cw(t) with us
= qw(t)/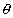w
and so the constant 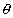w
is replaced with qw(t), a given time series for the percolation or
Darcy flux. This time series was determined from percolation analyses using site
precipitation data records (6). A constant w is still assumed, consistent with
small changes observed about the empirical value, and the transient flux is
given by Eq. 5. Results from the transient analyses are seen in Fig. 3 and 4.
Figure 3 (top) shows the normalized leachate concentration and percolation verses time and compares concentrations for the analytic solution to the averaged percolation rate (Cw-an-avg) and the numerical transient solution for the time dependant percolation (Cw-num-q(t)), for a particular percolation data 50 yr record. The percolation is very aperiodic and leads to correspondingly aperiodic changes in release concentrations which vaquely approximate the smooth curve result for the average percolation rate. This particular percolation data series is unusually dry for the first 25 years, and the transient leachate concentration is displaced accordingly to later times than the solution to the average percolation case.
Figure 3 (bottom) shows normalized leachate concentration verses time comparing concentrations for the analytic solution to the averaged percolation rate for a single 50 yr percolation record (Cw-an-avg) and for the average of four 50 yr percolation records (Cw_an_qave) and the numerical transient solution for the time dependant percolation averaged over four 50 year time series of percolation data (Cw_q(t)). The average percolation for each of the four 50 yr records ranged from 3.8 mm/yr to 9.1 mm/yr and the average over the four records is q = 6.7 mm/yr. The average percolation in the single 50 yr record plotted in the figure is 5.6 mm/yr. Since the average of this single 50 yr record is close to the average of the four records, the two smooth curves are similar however, they would vary in direct proportion to the average percolation over the range from 3.8 mm/yr to 9.1 mm/yr, depending upon the actual time series. The transient solution to the percolation averaged over the four 50 yr records is already beginning to approach the smooth curve given for the average percolation value in the analytic solution.
The waste package efflux corresponding to the concentrations in Fig. 3 is shown in Fig. 4 for the same percolation records. Normalized waste package leachate flux verses time (Fig. 4 (top)) compares values for the analytic solution to the averaged percolation rate (flux-w-q(ave)) and the numerical transient solution for the time dependent percolation (flux-w-q(t)). The transient flux, given by Eq. 5, is very different from the analytic solution to the averaged percolation rate, owing to the direct dependence of flux on the aperiodic Darcy flux, q(t). The transient flux is nearly an order of magnitude larger than the averaged value at some points in time but occurs only during the occasional percolation years.
Figure 4 (bottom) shows the normalized waste package leachate flux verses time, comparing flux for the analytic solution to the averaged percolation rate for the single 50 yr percolation record (flux-w-q(ave)) and for the average of the four 50 yr percolation records (flux_qave) and the numerical transient solution for the time dependant percolation averaged over four 50 year time series of percolation data (flux_q(t)). The numerical solution to the transient case for the average of the four records is slowly approaching the analytic solution to the average percolation, however, the transient fluxes still differ from the average case typically by a factor of two and they occur only in the percolation years. Here, the averaging produces flux greater and less than the average flux value while the actual result for a single percolation record will always exceed the average during percolation years and will be equal to zero in this simple model during years without percolation.
DISCUSSION
Transient results show that in conditions approaching the extreme case,
which might represent a waste package in a relatively shallow portion of the
disposal unit, that the waste source release term fluctuates considerably and is
aperiodic in time following the particular time sequence of the moisture pulses
following individual percolation occurences. The model however does not
represent these extreme conditions accurately because the moisture transit time
past a waste package, Tw = hw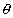w/qw(t), is
assumed constant in space and is assumed to vary in time only through qw(t).
Actually, there will be variations in space and time associated with each waste
package, i.e., qw(z,t) and
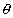(z,t) will vary in time and in
space even over the distance associated with the waste package height, hw.
This will tend to average the waste leachate efflux over the transit time and
will dampen fluctuations on time scales shorter than the transit time, T = hw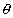w/qw(t) ~ 16
years in the case for Area G. On the other hand, the transit time for averaging
a typical transient (4cm/yr for one year) is much less, T = (1)(0.08)/0.04) = 2
yr.
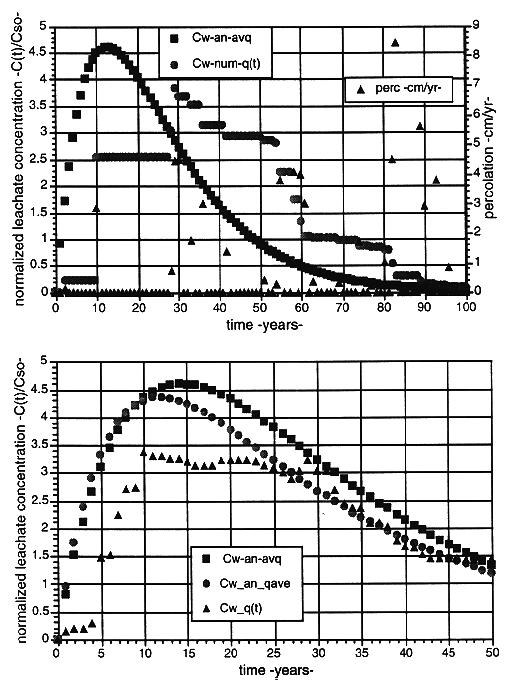
Fig. 3 (top) Normalized leachate
concentration and percolation verses time comparing concentrations for the
analytic solution to the averaged percolation rate (Cw-an-avg) and the numerical
transient solution for the time dependant percolation (Cw-num-q(t)).
Fig. 3 (bottom) Normalized leachate concentration verses time comparing
concentrations for the analytic solution to the averaged percolation rate for a
single 50 yr percolation record (Cw-an-avg) and for the average of four 50 yr
percolation records (Cw_an_qave) and the numerical transient solution for the
time dependant percolation averaged over four 50 year time series of percolation
data (Cw_q(t)).
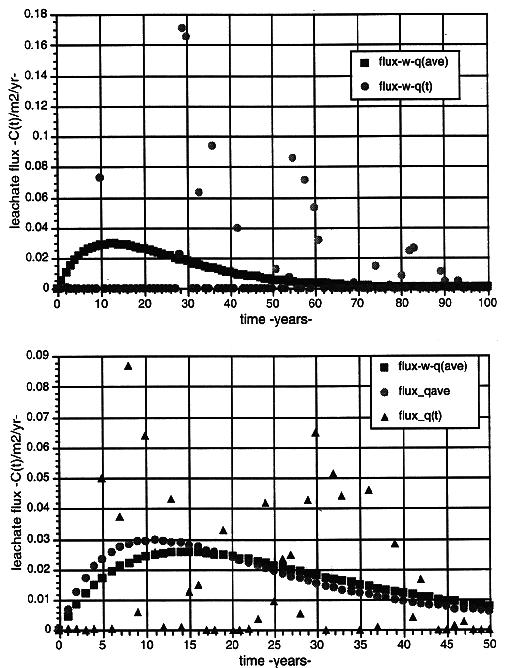
Fig. 4 (top) Normalized waste package
leachate flux verses time, comparing values for the analytic solution to the
averaged percolation rate (flux-w-q(ave)) and the numerical transient solution
for the time dependant percolation (flux-w-q(t)).
Fig. 4 (bottom) Normalized waste package leachate flux verses time, comparing flux for the analytic solution to the averaged percolation rate for a single 50 yr percolation record (flux-w-q(ave)) and for the average of four 50 yr percolation records (flux_qave) and the numerical transient solution for the time dependant percolation averaged over four 50 year time series of percolation data (flux_q(t)).
As the depth of disposal increases, releases from the waste are expected to
approach projected releases based on the steady-state percolation rate. Field
data and numerical calculations on variations in moisture content profiles in
the near surface unsaturated zone suggest that the percolation fluctuations
dampen near the surface and that below about 2 m depth the variations are slight
(10) and approach the averaged conditions assumed in the steady state model.
Waste packages at different locations throughout the disposal unit will see the
moisture transients at various phases of the passing moisture pulse. Leachate
efflux from the disposal unit will be averaged over the differences associated
with the larger disposal unit volume and will tend to dampen fluctuations on
time scales shorter than T = hd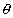d/qd(t), where subscript d
refers to 'disposal unit', and the typical height, hd is 20m, thus tending to
average out fluctuations on time scales less than about 300 years.
The results show that the transient solution approaches the analytic solution for the average percolation rate as the percolation sequences are averaged in time. This has two implications. One, the variations for a set of particular percolation sequences represent the envelope of expectations for what will actually occur in the next 50 years which will drive the release from the disposal facility. At the end of site operations, the actual precipitation and percolation data could be used to estimate the actual release. There is a second implication of the transient results if we also assume that the averaging in time is related to averaging in space. The variability in percolation at different points in space is known to be large (7). If we assume this indicates a real variation over an area comparable to that of a disposal unit then the net efflux from the area of a disposal unit is an average and the actual percolation over space and time will approach that averaged solution for the 'time average' percolation rate. Within and beyond the volume of the disposal unit, hydrodynamic dispersion will also act to average transients during transport to dose receptor sites.
APPLICATION TO THE AREA G SITE PERFORMANCE ASSESSMENT
The Area G inventory is divided into four segments based on the time of disposal 1959 to 1970, 1971 to 1988, 1988 to 1995, and 1996 to 2044) for dose consequensus analyses. The waste disposed of between 1988 and 2044 is included in the Area G Performance Assessment compliance evaluation. All of the waste is considered in analyses which partially satisfy DOE 'Composite Analysis' requirements for active disposal facilities. The four inventory groups are distinguished roughly as: 1959-1970; limited TRU-LLW segregation, no detailed data base records, inventory by extrapolation, 1971-1988; detailed data base for inventory, TRU and LLW distinguished, pre-compliance period, 1988-1995; detailed inventory data base to present date, compliance-driven, 1996-2044; future operations projected throughout the expected lab lifetime, compliance-driven. Inventory from 1971-1995 is segregated by disposal unit for the source release model and for the subsequent transport analyses, distinguishing over 30 disposal pits and four grouped 'shaft fields'. Extrapolated inventory (<71 and >96) is averaged over (past and planned) disposal units.
For each of the source term disposal units, the rapid release component of
the waste inventory is specified by waste quantity, Qo(Ci), and
waste package volume, V(m3). The curie concentration is converted to
molar concentration and the maximum leachate concentration, Cw-max =
(0.37Cso/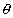 ), is
compared to the elemental solubility limit. Where Cw-max is less
than the solubility limit, the nuclide is considered to be inventory limited and
the integrated release from the waste packages,
w,
for a particular nuclide from each disposal unit is calculated by integrating
Eq. 4 over waste package area to obtain,
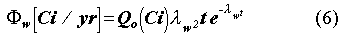
This release (and subsequent maximum concentrations and dose assessments) depends upon inventory quantity but is independent of inventory volume or concentration.
If Cw-max is predicted to exceed the elemental solubility limit, Csl, the total leachate concentration by element will be limited to Csl and the actual leachate concentration by nuclide will be some fraction of Csl where the fraction, fsl, depends upon the contributions to that elemental solubility limit from other nuclides of the same element. The integrated leachate flux from the waste packages during the solubility limited release is
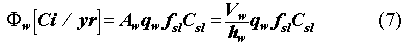
The duration,
tsl,
of release at this rate is
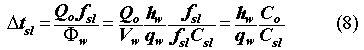
Following this duration, the release will be briefly inventory limited and
follow Eq. 6. This leads to a rapid decrease in release rate and so the
solubility limited release rate can be realistically approximated as a step
function with step height given by Eq. 7 and duration ending at
tsl.
This release for solubility limited nuclides scales as the total nuclide
inventory volume, Vw, because the release rate is limited to the
fixed concentration, Csl. The initial waste concentration (at
disposal time), Co = Qo/Vw, does not play a
direct role in the integral source strength for either release case, but does
determine the duration of a solubility limited release.
Previous analysis (3) indicated that only a few nuclide elements which were shown to be of significance in the site dose assessment were also consistently solubility limited. These included uranium and thorium. The nuclide fraction of the solubility limit, fsl, is found to be an important correction only for the uranium inventory. Extending the previous analysis to individual disposal units identifies specific pits and shafts where solubility limits are exceeded. Plutonium and americium become solubility limited in a few disposal units including the shaft fields, often reserved for disposal of waste with greater specific activity. The realistic spatial distribution of the disposal units with the individual source terms which are either inventory or solubility limited serve as input to the detailed 3-D unsaturated zone modeling effort underway as part of the performance assessment (8).
CONCLUSIONS
Phase Two source release modeling acknowledged previous results that the 'rapid release' waste category is critical, and therefore deserves a more self-consistent treatment of the percolation and transition from the solid to the liquid phase in the waste package leachate. This leads to new analytic expressions for the case of inventory limited release which has been applied to the Area G Site Performance Assessment in calculations incorporated directly into the 2-D and 3-D unsaturated zone transport model. Elemental solubility limits dictate which nuclide waste is 'inventory-limited' and which is 'solubility limited' on an individual disposal unit basis. The integrated release for the inventory limited case is proportional to the total inventory in a given disposal unit while the solubility limited release is proportional to the inventory volume and the solubility limited duration is proportional to the waste inventory concentration.
Transients in release rates due to time varying percolation rates were examined and found to potentially impact the results considerably. The results bracket the uncertainty due to percolation, but probably overestimates the variability in the real case. The release model does not accurately represent some detailed aspects of the transient case and many factors in the real situation, including hydrodynamic dispersion and spatial and temporal variability in percolation, are likely to average the actual release rates and tend to smooth the results towards those predicted by the analytic model using the average percolation rates.
ACKNOWLEDGMENT
This work is sponsored by the U.S. Department of Energy, Waste Management Program Office.
REFERENCES