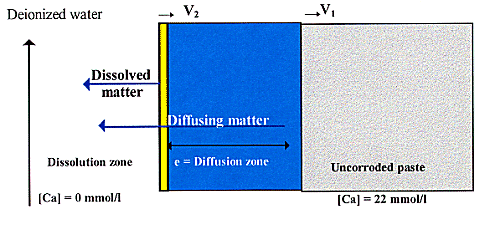
Fig. 1. Mechanisms of degradation in
a cement paste (V1: speed of advance of diffusion boundary, V2:
speed of advance of dissolution boundary).
P. Faucon
Service de Physique de l'Etat Condensé,
C.E.A Saclay, 91191 Gif sur Yvette, France and Université Cergy-Pontoise,
Laboratoire Matériaux et Sciences des Constructions
I.U.P Génie
Civil et Infrastructures, Rue d'Eragny, Neuville sur Oise, 95031 Cergy Pontoise
Cedex, France
F. Adenot
Service d'Entreposage et de Stockage des
Déchets, C.E.A Saclay, 91191 Gif sur Yvette, France
J.F
Jacquinot
Service de Physique de l'Etat Condensé, C.E.A Saclay,
91191 Gif sur Yvette, France
R. Cabrillac
Université
Cergy-Pontoise, Laboratoire Matériaux et Sciences des Constructions
I.U.P Génie Civil et Infrastructures, Rue d'Eragny, Neuville sur Oise,
95031 Cergy Pontoise Cedex, France
F. Pineau and M. Jorda
Agence
Nationale pour la Gestion des Déchets Radioactifs, 92298 Châtenay-Malabry,
France
ABSTRACT
During development studies of a site for the storage of highly radioactive waste, we examined the degradation of several cement pastes by completely demineralized water. In the short term, degradation results from transport of matter between the sound zone and the aggressive solution by diffusion of ionic species from the interstitial solution of the cement paste.
After a critical time, which depends on the type of paste, the dissolution of the surface layer in contact with the aggressive solution will determine the kinetics of degradation. Unlike diffusion, surface dissolution accelerates and then becomes constant, and must therefore be limited.
Dissolution of the surface layer is principally controlled by its solubility. The presence of trivalent iron in the paste considerably reduces this solubility and slows dissolution. In deep storage sites, where the water is not continually renewed, the critical time will never be reached if calcium solubility is low enough.
INTRODUCTION
Cement is often used to contain nuclear waste of medium and high activity, and can also be employed as a barrier structure in the design of a storage site. To ensure the safety of disposal sites it is therefore essential to understand fully the mechanisms of cement degradation. In the case of disposal several hundred metres below ground, one worst-case scenario is leaching of the cement by demineralized water. That is why it is necessary to study this event to evaluate the conditions for a slowest kinetics of degradation.
Cement paste comprises hydrates in equilibrium with an interstitial solution in the pores of the material. These hydrates are stable at calcium concentrations around 22 mmol/l in the absence of alkalis [1]. The water-degradation of a cement-based structure can then be decomposed into two mechanisms.
The first mechanism results from the concentration gradient created between the surface of the cement structure, in contact with the aggressive solution of [Ca2+]=0 mmol/l, and the core of the structure [2,3]. The Ca2+ ions of the interstitial solution diffuse from the core towards the surface of the structure (Fig. 1). In this diffusion zone, the chemical equilibria are modified, resulting in dissolution and precipitation [3]. These chemical reactions occur faster than diffusion, which they therefore cannot slow [2]. Assuming that the region in contact with the aggressive solution does not dissolve, the kinetics of degradation will then be determined by diffusion [4].
The second mechanism results from the dissolution of the surface layer in contact with the aggressive solution [5]. This dissolution causes shrinkage of the interface, thereby compromising the cement structure (Fig. 1).
In practice, these two mechanisms are coupled. Our aims in this paper were to determine the parameters controlling the surface dissolution, to study the diffusion-dissolution coupling and to evaluate the long-term behavior.
Fig. 1. Mechanisms of degradation in
a cement paste (V1: speed of advance of diffusion boundary, V2:
speed of advance of dissolution boundary).
EXPERIMENTAL CONDITIONS
The influence of the composition of the cement on the kinetics of degradation was studied in four cement compositions. Samples 1 to 3 (Table I) were prepared from C3S (C=CaO, S=SiO2), synthesized by Ciments Français. The influence of iron was studied by the addition of iron nitrate (FN). When nitrates were introduced, they were neutralized by addition of CaO. The last cement composition was an ordinary Portland cement (OPC) from the Altkirch factory of Ciments d'Origny.
Table I Sample Composition (% of mass)
Samples 7 mm in diameter with a water/cement ratio of 0.38 were kept for one month in a solution saturated in portlandite, before leaching by a pH 7 solution deionized by recirculation through a mixed bed of ion-exchange resins. The tests were performed under an inert atmosphere (N2).
Sample diameter before degradation and at various time-points (15 days, 1 month, 45 days, ...) was measured to within ± 20 microns using a numerical micrometer. This allowed us to monitor shrinkage as a function of time.
After three months of leaching, the surface layer (50-100 microns) was removed, and a 250 mg sample (about 0.1 ml of solid) was placed in 15 ml of water. Changes in calcium concentration were monitored in order to study the kinetics of dissolution of the zone in contact with the aggressive solution.
EXPERIMENTAL RESULTS
Shrinkage
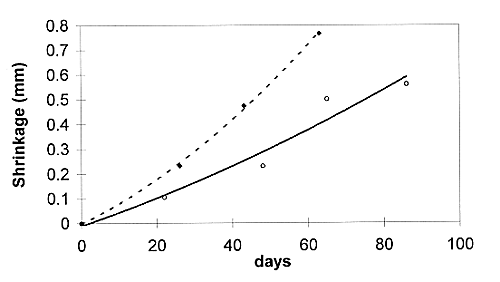
Fig. 2. Shrinkage of the interface as
a function of time.
Figure 2 shows the shrinkage as a function of time for samples 1 to 3.
Shrinkage caused by the dissolution of matter in contact with the aggressive
solution was substantial in the pastes prepared from C3S. The rate
of shrinkage seemed to increase, unlike diffusion mechanisms which obey a 1/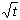
law. In the long term, the
dissolution of the degraded layer is therefore likely to determine the rate of
degradation of the paste. The composition of the paste considerably influences
the rate of shrinkage, which was slowed by iron nitrate.
No significant shrinkage of the OPC paste could be measured after three months of degradation.
Kinetics of dissolution of the surface layer.
In general, the kinetics of dissolution of a unit volume of matter can be written as:
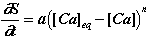(1)
where S is the quantity of matter in the unit volume of solid, t the time, a the dissolution kinetics constant, [Ca]eq the steady-state calcium concentration, and n the order of the reaction.
To measure these different parameters we removed a quantity S
from the surface layer and placed it in a fixed volume of water. In this volume,
the dissolution of
ns
moles of calcium increases the calcium in solution by
nL
moles:
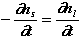(2)
As ns = S VS and nL = [Ca] VL, where VS = volume of solid introduced and VL = volume of liquid, hence:
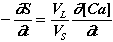(3)
Equations (1) and (3) can be used to write:
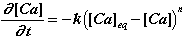(4)
where k =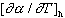 
When the kinetics are second order (n=2), the solution of this differential equation yields the expression:
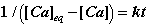(5)
When 1/([Ca]eq-[Ca]) was plotted as a function of time (Fig. 3), the second order kinetics were confirmed, and we measured k, and hence a, which characterize the kinetics of dissolution. For reasons of clarity, we have only represented the results obtained for the C3S paste and the OPC paste. The kinetics constant is virtually the same for all the degraded surface layers:
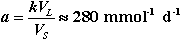(6)
The kinetics of dissolution are therefore the same, irrespective of the initial composition of the paste. In contrast, the solubility of the different species at steady-state is a function of paste composition (Table II).
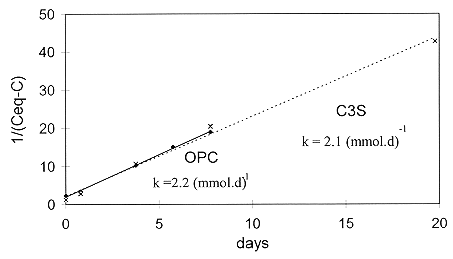
Fig. 3. Steady-state kinetics of the
surface layers (1/([Ca]eq -[Ca]) as a function of time)
Table II Steady-State Calcium Solubility in the Surface Layers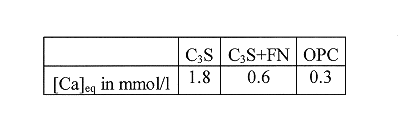 
LONG-TERM BEHAVIOR
Our aim here is not to propose a complete model describing all the physicochemical processes occurring during leaching, but rather to evaluate the thickness of the degraded layer as a function of time when a cement paste is attacked by completely demineralized water.
Parameters determining surface dissolution
Once the equilibrium concentration of one of the ions in the surface layer (Table II) differs from that in the aggressive solution, dissolution of the ion will begin. For a concentration "C" ([Ca], [Si], or [Al]) in the aggressive solution which is below the solubility "Ceq" of the surface layer, the kinetics of dissolution of a unit volume of the surface layer can be written:
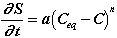(7)
This dissolution will be less for small distance (Ceq-C) from thermodynamic equilibrium. The order of the reaction "n" and the kinetics constant "a" will theoretically be of great importance. However, measurement of these two coefficients (Fig. 3) shows that they are identical for different pastes and are therefore difficult to reduce. They seem to be an intrinsic characteristic of the surface layer. The distance from thermodynamic equilibrium will then be the fundamental parameter.
Diffusion regime
At the start of degradation, shrinkage can be neglected. The thickness of the degraded layer "e" is determined by diffusion and is a function of t [2,3]:
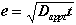(8)
where Dapp is a uniform coefficient of diffusion.
Dapp can be evaluated as 15,000 µm2/day from the results recorded by Adenot for an OPC paste [2].
If V1 is the speed of advance of the diffusion zone boundary, it can be expressed as:
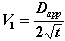(9)
As degradation continues, a critical time "t0" is reached beyond which shrinkage of the interface must be taken into account.
Notion of critical time
The surface layer is not in thermodynamic equilibrium, and will therefore
shrink at a rate that increases or is constant (Fig. 1). The shrinkage will
therefore be too great to be neglected. The thickness of the degraded layer will
then no longer be a function of ,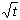
but rather will increase much faster. We shall define "t0" as the time
for which the rate of shrinkage "V2" equals V1.
The expression of t0 is a function of the rate of shrinkage of the
interface during the diffusion regime.
Modeling of shrinkage as a function of time
In the case of completely demineralized water, all leached species must be taken into account. For this sort of attack, the equilibrium conditions cannot be reduced to a single species describing the system. To simplify the problem, we shall only take into account the distance from thermodynamic equilibrium in terms of calcium concentration. All the surface layers have a high calcium solubility, and so the distance (Ceq-C) from thermodynamic equilibrium (Table. II) will be the greatest for this ionic species.
We divide the leached sample into two distinct zones. The first corresponds to a diffusion zone in which there is local chemical equilibrium and whose speed of advance is V1. As soon as the calcium concentration in the surface layer falls below Ceq (equilibrium [Ca] in the surface layer), the second, or dissolution zone begins. Its boundary advances at a speed of V2 (Fig. 1). Since the aim is to determine the change in V2 during the diffusion regime, V2 will be considered negligible compared with V1. The thickness of this zone, "e", will therefore be given by expression (9).
In a porous medium where diffusion and dissolution-precipitation occur, Fick's second equation becomes [6]:
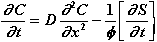(10)
Where C is the calcium concentration (in our case) of the interstitial
solution at a point in the dissolution zone, expressed in mmol/l, D is the
coefficient of diffusion of calcium in the dissolution zone, is the porosity of
the dissolution zone,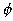 
is
the calcium concentration of the solid phase at a point in the dissolution zone,
expressed in mmol/l of solid.
D and 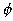are assumed to
be constant in the dissolution zone. This assumption is not strictly true, and
will tend to diminish the influence of the dissolution.
Using expression (1), and knowing "a" and "n", we have:
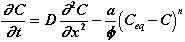(11)
This equation can only be solved numerically and, in practise, n=2 (second
order kinetics: Fig. 3). Like Adenot [2], we adopted a value of 0.6 for
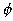in the surface layer. The
coefficient of diffusion of tritiated water in a thin layer of OPC of
water/cement ratio 0.5 was chosen for D (3,000,000 µm2/day). Cpaste
was taken as 22 mmol/l. The calcium concentration in the surface layer (S0)
is initially 6,000 mmol/l. This value takes into account the fact that only
about 10% of the calcium remains in the paste in the surface layer [5].
Figure 4 shows how V2 changes as a function of time for different Ceq values. In all cases, V2 increases with time, as Fig. 2 appeared to indicate. However, when V2 approaches V1, it decreases and seems to stabilize.
For Ceq =1.8 mmol/l, a value corresponding to the surface layer of the C3S paste (Table II), V2 very quickly becomes roughly equal to V1. The critical time "t0" is then reached after about two weeks. V2 is then about 10 microns/day, a value in agreement with our experimental observations.
The drop in Ceq from 1.8 mmol/l to 0.6 mmol/l results in a sharp decrease in V2. The critical time is then a few months. At three months, the rate of shrinkage is similar to that observed experimentally for the C3S + iron nitrate paste, whose calcium solubility is 0.6 mmol/l (Fig. 2).
For Ceq = 0.3 mmol/l (case corresponding to the OPC paste), the V2 again decreases considerably by comparison with the case Ceq = 0.6 mmol/l. The halving of the equilibrium concentration of the surface layer results in a 10-fold increase in the time to onset of the critical regime.
Fig. 4: Rate of shrinkage of the interface (V2) for different Ceq .
Table III Critical Time as a Function of Ceq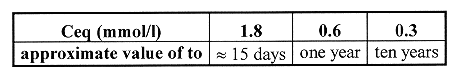 
Table III recapitulates the critical times for the different Ceq. In the scenario of attack bycompletely demineralized water, the diffusion regime will constitute a relatively short transitory period: the more soluble the surface layer, the shorter this period. For example, if the calcium solubility is lowered from 1.8 mmol/l to 0.4 mmol/l, the time to onset of the critical regime will increase from a few days to tens of years.
Once the critical regime is established, the rate of shrinkage should stabilize and become constant. Degradation will then occur at a rate that is a linear and not a function of t. This rate will be slower at lower values of Ceq. For an OPC paste, this rate could be about 0.5 µm/day (for t > t0), compared with above 10 µm/day for the C3S paste.
Influence of the composition of the paste on Ceq.
Faucon et al. [7,8] have shown that the surface layer of degradation of an OPC paste attacked by pure water mainly comprised calcium silicate hydrates (CSH), of molecular structure close to that of tobermorite, and in which part of the calcium exchanges with trivalent iron. The formation of these Fe-CSH seems to be one of the keys to the durability of the material. Indeed, in the C3S paste, the absence of iron prevents formation of these Fe-CSH. The calcium solubility of the surface layer in contact with demineralized water is then 1.8 mmol/l (Table 2). If trivalent iron is present in the system, this solubility is lowered to 0.6 mmol/l (C3S+FN paste), and even to 0.3 mmol/l (OPC paste). The precipitation of Fe-CSH in the degraded layer considerably reduces the rate of shrinkage and hence increases the time to onset of the critical regime.
CONCLUSIONS
This study clearly demonstrates the fundamental role of the surface layer in contact with the aggressive solution. When the surface layer is not in thermodynamic equilibrium, its kinetics of dissolution will determine the degradation of the material. Degradation will be greater if the surface layer is more soluble. Durability is poorer in the absence of trivalent iron in the paste.
In terms of the disposal site for nuclear waste, the flow rate of the aggressive solution will likely be very low. Assuming that the water is completely demineralized, it will take up ionic species from the interstitial solution of the cement paste. If the different solubilities of the surface layer are very low, this steady-state will be reached easily and will be maintained for a long period. As the calcium solubility is generally the highest, trivalent iron will be added to the paste. Its incorporation into the CSH of the surface layer will reduce calcium solubility four-fold. The surface layer will then be in thermodynamic equilibrium and will not dissolve. With a zero rate of shrinkage, the diffusion regime will continue. OPC paste will constitute a valuable material in this regard.
REFERENCES