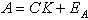 (1)
(1)
Michael A. Power
Engineering Division
Argonne
National Laboratory
P.O. Box 2528
Idaho Falls, ID 83403-2528
Oleg O. Tolstikhine
College of Engineering
Idaho
State University
P.O. Box 8895
Pocatello, ID 83209
Kevin P. Carney
Engineering Division
Argonne
National Laboratory
P.O. Box 2528
Idaho Falls, ID 83403-2528
ABSTRACT
Argonne National Laboratory, Science Applications International Corporation and Lockheed Martin Idaho Technologies are developing a Plasma Hearth Process (PHP) which will process mixed hazardous and radioactive waste. The goal of this work is to convert the Infra-Red (IR) spectrum of the PHP off-gases into CO concentration data using neural network and Partial Least Squares (PLS) techniques, and to determine which technique produces a more accurate estimate of the CO concentration. The neural network technique produces a more accurate estimate of the CO concentration in that the sum-squared relative error and the worst-case relative error are smaller. The research is obtained using non hazardous, non radioactive waste since the PHP is not yet used to process hazardous, radioactive waste.
INTRODUCTION
The goal of the PHP is to process mixed hazardous and radioactive waste by decomposing hazardous organic materials, by encapsulating actinide waste in an obsidian-like slag, and by reducing storage volume of actinide waste. The CO concentration data obtained for this work is for non hazardous, non radioactive waste since the PHP is not yet used to process hazardous, radioactive waste.
The Introduction briefly describes the processing of the waste. Section II describes the Partial Least-Squares method used to convert the IR spectrum into the estimated CO concentration. Section III describes the neural network techniques used to convert the IR spectral data into the estimated CO concentrations. The comparison of the PLS technique and the neural network technique in Section IV demonstrates that the neural network technique produces a smaller error and therefore a more accurate estimate of the CO concentration.
The PHP torch chamber consists of a plasma torch at the top of the chamber which heats the gases that actually melt the waste, a hydraulic ram which pushes the waste into the torch chamber, and a crucible at the bottom of the chamber which catches the drip-melted waste. The plasma torch generates a plasma with a peak temperature of 10,000°F. The plasma heats the gases within the torch chamber, and then the heated gases melt the cans of organic and actinide contaminated waste pushed into the torch chamber by the hydraulic ram. The waste drip-melts into the crucible. Organic materials (e.g., PVC, C6H4Cl2, etc.) decompose in the thermal environment of the plasma torch. Possible actinides in the waste may preferentially migrate to the slag phase of the melt (e.g., a mixture of Alumina, Magnesia, and Silica) where the actinides may be captured when the waste cools and hardens. (1) The slag is suitable for encapsulating the actinides for long-term disposal. Since the slag may occupy a smaller volume of the entire melt, the effective storage volume of waste may be reduced.
The PHP has a special off-gas system capable of accepting radioactive, contaminated particulate streams. The off-gas system consists of a secondary combustion chamber, a quench, a HEAP filter bank, and an acid scrubber. The secondary combustion chamber contains a propane fueled torch which thermally decomposes any residual organics emanating from the plasma hearth. The quench reduces the gas temperature from the secondary combuser to levels below 450°F. The gases pass through the quench and then into the HEAP filter bank. The HEAP filter bank consists of a dust filter and a secondary HEAP filter which removes radioactive contaminated particles from the off-gas. Once the off-gases leave the HEAP filter bank, the off-gases pass through an acid scrubber which absorbs acidic gases such as HCl. Finally, the off-gases flow into the facility stack.
The off-gas system is monitored using a Fourier-Transform Interferometer (FTIR) for inorganic and organic compounds, a Laser-Induced Breakdown Spectroscopy system (LIBS) for actinides, and a Two-Color Transmisometer (TCLT) for microparticles. The FTIR provides on-line spectral data for the products of waste combustion, namely CO, H2O, CO2, NOx, SO2 and HCl. The Laser-Induced Breakdown Spectroscopy system (LIBS) generates spectral data for metallic particulates, namely U, Pu. The Two-Color Transmisometer (TCLT) provides particle size and density data.
The FTIR detector consists of a Midac interferometer and a SiC light source. The SiC light source produces photons which travel though the off-gas flow and impinge upon the Midac interferometer. The Midac interferometer collects an interferogram which is then converted into an absorbance spectrum. The absorbance spectrum is converted into concentration data using PLS and neural network techniques. The process of collecting an interferogram and estimating the CO concentration takes on average 1 minute. The Midac interferometer is connected to a data collection PC. The data collection PC uses the MDGRAMS program to collect interferograms to convert interferograms into spectra. The spectra are transferred to a Sun microcomputer using a local ethernet connection. A MATLAB program running on the Sun computer reads the spectra and converts the spectra into concentrations. The concentrations and incoming spectra are then stored and displayed on the Sun computer.
When the LIBS system is operational and is working on-line, the system will use the same routine for data processing.
Unlike the FTIR and the LIBS detector which do not process data locally, the TCLT processes the raw data from the TCLT detector locally. The processed data is then transferred to the Sun computer for storage and display. The TCLT detector determines particle size and density of the off-gases. The detector is located between the quench and the HEAP filter bank.
CLASSICAL AND PARTIAL LEAST-SQUARES ANALYSIS
The Partial Least-Squares method is used to convert the IR spectrum into the estimated CO concentration. The Partial Least-Squares method is derived from the Classical Least-Squares (CLS) method. The CLS method assumes Beer's law in which the absorbance at each frequency is proportional to the component concentration. The Beer's law model assumes the modeling error is solely due to the error in spectral absorbances. In matrix notation, Beer's law is written as:
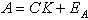 (1)
(1)
where
A = m x n matrix of calibration spectra
C = m x l matrix of component concentrations
K = l x n matrix of pure-component spectra at unit concentration and unit path-length
EA = m x n matrix of spectral residuals.
and
m = number of calibration standards
l = number of chemical compounds
n = number of absorbance spectra.
The CLS solution for K minimizes the squared spectral errors from EA,
yielding the estimate 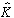
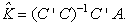 (2)
(2)
The CLS estimate of 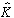 in
Eq. (2) is used to estimate the CLS concentration
in
Eq. (2) is used to estimate the CLS concentration
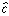
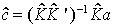 (3)
(3)
where a is the unknown input spectrum.
The partial least-squares method, derived from the CLS method, assumes a similar model
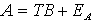 (4)
(4)
where
A = m x n matrix of calibration spectra
B = h x n matrix with the rows of B being the new PLS basis set of h full spectrum vectors
T = m x h matrix of intensities in the new coordinate system of the h loading vectors for the m sample spectra
EA = m x n matrix of spectral residuals.
The intensities in the new coordinate system (the new basis of h calibration spectra) are no longer the concentrations as they were in the CLS method, but they can be modeled as linearly related to concentrations by the following equation
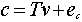 (5)
(5)
where
c = m x 1 concentration matrix
T = matrix of intensities from the PLS decomposition in Eq. (4)
v = h x 1 vector of coefficients relating the intensities to the concentrations.
The explanation of the estimation of T, B and the concentrations is too laborious for this work, but the mathematics may be investigated in the Haaland and Thomas article. (2)
Whereas the partial least-squares technique uses linear matrix transformations to estimate concentrations, the neural network technique uses a hierarchical structure of nonlinear functions to estimate concentrations. In Section III, neural networks produce less estimation error than PLS.
NEURAL NETWORK ANALYSIS
Neural networks have been successfully applied to pattern recognition problems. Since the estimation of concentration from spectra is essentially a pattern-recognition problem, neural networks can be used to convert the IR spectral data into the estimated CO concentrations. The general form of the neural network is presented along with the learning rule used to train the network. A radial basis network requires less time to train the network and is therefore used in this work. (3)
The neural network has the general form
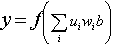 (6)
(6)
where
y = network output
f = arbitrary function
ui = ith network input
wi = ith network weight
b = network bias.
In general, the neural networks are interconnected to form input layers, hidden layers, and output layers. The input layer for the concentration estimation is 1 x n for n absorbance spectra, and the output layer is 1 x m for m output concentrations. The size of the hidden layer depends upon the complexity of the estimation.
The radial basis neural network fixes the choice of function f, defined as
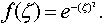 (7)
(7)
The learning rule for the radial basis network uses least squares regression to interatively search for the weights wi and the biases bi which minimize the sum squared error. The learning continues until the sum-square error falls below a prescribed tolerance. The tolerance for the sum-squared error in this work is 0.01.
EXPERIMENTAL RESULTS
Infra-red Spectra were collected for various known concentrations of CO. The spectral data were processed using the neural network technique and the PLS technique. A comparison of the estimated concentration shows that neural network technique generates a smaller worst-case and sum-squared error than the PLS technique.
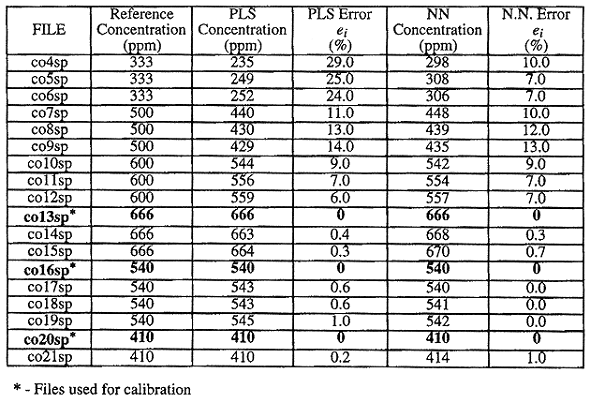
Table I compares the actual concentration of CO to the estimated concentration of CO for both the PLS and neural network techniques. Files number co13sp, co16sp, co20sp are the spectra used for calibration of the two techniques. The resulting estimation error is exactly zero for these three spectra. At higher concentration levels of CO, the neural network produces similar relative error to PLS, however, at lower concentration levels the neural network produces a substantially smaller estimation error than PLS.
Table I Comparison of PLS Routine vs. Neural Network (CO
Concentration Estimation)
Two performance measures which compare the estimation error between the neural network and PLS techniques are the sum-squared error and the worst-case error. The sum-squared error is defined as
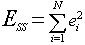 (8)
(8)
where
ei = ith error between the actual and estimated concentrations
N = number of reference spectra
and the worst-case error is defined as
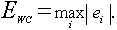 (9)
(9)
The summed-squared error for the neural network technique is 892 and the summed-squared error for the PLS technique is 2,285. The worst case error for the neural network technique is 13.0 and the worst case the error for the PLS technique is 29.0. Both measures show that the neural network produces a more accurate estimate of the CO concentration in excess of a factor of two.
CONCLUSIONS
Infra-red spectral data was collected from the PHP off-gas system. The neural network and PLS methods were used to estimate the concentration of CO in the spectral data. The neural network method produced a better overall estimate of the CO concentrations in terms of the squared-error and the worst-case error.
Future work may use the FTIR and LIBS detectors for closed-loop control. Since the FTIR detector determines the concentrations of the products of combustion, the detector can be used to optimize burner efficiency. Since the LIBS detector measures actinide entrainment in the off-gas, this measure may be used to control the waste feedrate and plasma torch flows in order to minimize the entrainment of actinides in the off-gasses.
REFERENCES