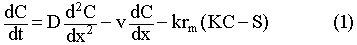Ernest Hardin and Randy Bassett
The University of
Arizona
Michael Murrell
Los Alamos National Laboratory
ABSTRACT
Waterrock interaction involving uranium was investigated by isotopic analysis of 238Useries nuclides in pore water and secondary minerals. Samples of secondary U were obtained by selectively leaching intact rock samples, and by digestion of fracture lining minerals, from the Apache Leap Tuff. Leaching was used in order to preserve the structure of the waterrock interface. Leachates analyzed by mass spectrometry with isotope dilution, were found to contain much more U than present in pore water, yet with similar 234U/238U activity ratios. In principle these observations could have resulted solely from U coprecipitation with secondary minerals such as manganese oxides, but a model incorporating isotopic exchange provides a plausible alternative. Both coprecipitation and isotopic exchange hypotheses lead to predictions of U retardation in situ, but isotopic exchange can operate continuously without requiring transport and precipitation of a carrier species.
Isotopic exchange between groundwater and a high affinity sorbent layer was treated analytically as retarded diffusive transport within the layer, and equated with a classical firstorder kinetic model to derive a rate constant representing layer diffusion behavior. Firstorder sorption rate parameters could then be calculated directly from laboratory selective leaching data, indicating that waterrock interaction is rate limited on the time scale of 234U decay (t1/2 = 245,000 yr). Similar results were obtained for intact core samples spanning the vadose zone at Apache Leap, representing a range of hydrologic conditions. These parameters can be used to compute rate dependent solute retardation in the rock matrix in situ.
The layer diffusion model was also applied to UTh analysis of fracturelining manganese oxide minerals from the Apache Leap Tuff. The 234U/230Th systematics indicated opensystem behavior, and the shift was consistent with isotopic exchange involving 234U. The fracturelining mineral samples were relatively thick, and the calculated rate constant values were small. This outcome was predicted qualitatively by the layer diffusion model, and shows that retardation involving high affinity sorbents encountered as fracturelining minerals at Yucca Mountain and elsewhere is strongly rate limited.
BACKGROUND
The 234U/238U activity ratio (AR) in pore waters of the Apache Leap Tuff increases from about 1.4 in runoff to > 6 in perched water (Fig. 1). Fractionation is correlated with an oxidative weathering horizon, and is apparently caused by the autooxidative selective leaching mechanism of Petit et al. (1). Manganeseoxides contain much of the secondary U present in this tuff, as shown from leaching studies on crushed rock (2). A corehole was airdrilled through the vadose zone, intercepting a perched water table at approximately 150 m depth. Core samples were analyzed for chemical composition, hydraulic and geophysical properties. Core was preserved in airtight packages, and later sampled for environmental isotopes by core squeezing and distillation (3). Intact core samples were leached with MilliQ water, then a solution of 0.1 M hydroxylamine hydrochloride and 3% acetic acid, to sample the U abundance and 234U fractionation in pore water and secondary manganese oxides. Leaching with hydroxylamine produced U in quantities far exceeding the U dissolved in pore water, yet with similar 234U/238U activity ratios (Fig. 2).
Fig. 1. Comparison of 234U/238U
activity ratios for waters from the Apache Leap Tuff, sampled by different
methods.
Fig. 2. Uranium mass and 234U/238U
activity ratio for early and late leaching splits, obtained using hydroxylamine,
for several core samples spanning the vadose zone.
The hydroxylamine leaching results can be interpreted to represent either isotopic exchange or coprecipitation. Apparent 234U/238U ages for the leached precipitates were calculated assuming: 1) congruent leaching; 2) minerals sampled by leaching were precipitated from pore waters with AR equal to that presently observed; and 3) minerals sampled by leaching were precipitated over a brief time period relative to their 234U/238U ages ("event precipitates"). The resulting apparent ages are shown in Table I.
Table I Apparent Age of Precipitates Sampled by Leaching of Intact
Core with Hydroxylamine
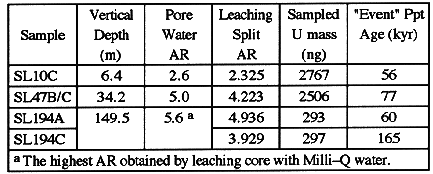
Similar apparent ages are obtained for samples from throughout the unit, and they are substantially less than the 246kyr half life of 234U. This similarity is the first line of evidence for isotopic exchange as a significant waterrock interaction process. Samples listed in Table I represent a wide range of hydrologic and chemical weathering conditions, yet the apparent ages are quite recent compared to the formation age (4). To the extent that precipitation is a continuous rather than "event" process, the apparent ages would be even less.
TRACTABLE FIRST ORDER MODEL FOR ISOTOPIC EXCHANGE
Waterrock interaction involving a highaffinity sorbent is modeled in terms of rate limited transport of U species within the sorbent. This layer diffusion model is equated mathematically to a firstorder kinetic model, using termwise comparison of series solutions (2). In this way the macroscopic effect of the entire layer on solute concentration in the mobile phase is described directly by a rate constant k, and a distribution coefficient K. These parameters can be used in a classical transport equation:
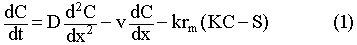
where D is a dispersion coefficient, v is the advective velocity, S is the immobile phase concentration, and rm is the rockwater mass ratio.
The observable quantity from which k and K can be deduced is the composite AR of secondary mineral precipitates, which can be sampled directly from fracturelining minerals, or sampled by leaching intact core. Although the model derivation shows that the effective rate constant for the entire layer is inversely proportional to the square of the layer thickness, it is not necessary to know the layer thickness in order to quantify k and K. The steady state AR of U dissolved in fracture water or matrix pore water is required for the calculation.
OBSERVATIONS INTERPRETED USING THE ISOTOPIC EXCHANGE/LAYER DIFFUSION MODEL
Using the leaching data of Table I, the matrix sorption parameters in Table II were calculated using an iterative scheme (2). Leaching may be incomplete, so the proportion of the sorbent layer dissolved congruently by leaching (p) is a variable in the problem. The U yield from leaching is known, so p is proportional to the whole rock distribution coefficient assuming that the pore water and the sorbent are in chemical equilibrium. Knowing the AR for two successive leaching splits from the same sample, and the pore water AR, it is possible to solve for the three parameters k, K, and p. As an example calculation, sorption parameters from Table II were used in a lumped parameter model to compute U retardation (Fig. 3).
Table II Sorption rate constant and distribution.
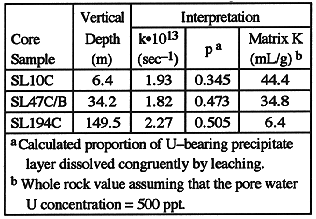
Fig. 3. Hypothetical curves for
uranium transport through tuff matrix, computed using sorption parameters
interpreted from laboratory leaching, and a lumped parameter model with
residence times as indicated.
The isotopic exchange/layer diffusion model was also used to modify the classical Useries relationship describing 230Th/234U/238U behavior in a mineral precipitated from pore water with known AR. The closed system "concordia" curve shown in Fig. 4 depicts the initial coprecipitation of fractionated U from solution without Th, which is insoluble. The initial 234U/238U activity ratio is greater than unity, and 230Th/238U is zero. As the precipitate ages there is ingrowth of 230Th, and the excess 234U decays toward secular equilibrium. Isotopic exchange causes the curves to shift, depending on the rate constant as shown. Each curve terminates along the diagonal line representing dynamic isotopic equilibrium. Loss of 234U from direct recoil (or selective leaching) causes a different shift in the curves as shown.
Fig. 4. Modified U-series condordia
plot showing the behavior of 234U and 230Th after
precipitation from a groundwater with known AR, under 234 Urecoil/leaching and
isotopic exchange conditions.
Three samples of fracture lining manganese oxides from Apache Leap were analyzed for 230Th/234U/238U by high resolution mass spectrometry, and found to plot along the steady state line in Fig. 4. This is the second line of evidence for isotopic exchange as a significant waterrock interaction process. Corresponding values for the sorption rate constant are smaller than those calculated for matrix sorption in Table II. The isotopic exchange/layer diffusion model predicts that the effective rate constant decreases significantly for thicker layers, which is the case for fracturelining precipitates. Thus although secondary fracture lining manganese oxide minerals are common in certain tuff units at Yucca Mountain, particularly hydraulically transmissive units in the saturated zone such as the Tram Member of the Crater Flat Tuff (5), the contribution of these phases to U retardation is strongly rate limited.
SUMMARY
Observations of U fractionation in secondary minerals of the Apache Leap Tuff can be evaluated in terms of coprecipitation or isotopic exchange. The hypotheses are inclusive, and both lead to predictions of U retardation in situ, but isotopic exchange does not require transport and precipitation of a carrier species, and is inherently plausible as a continuously operating retardation mechanism. Isotopic exchange explains the isotopic similarity of leachates from samples spanning the vadose zone at Apache Leap. A conceptual and numerical model of isotopic exchange is proposed based on retarded diffusive transport within a highaffinity sorbent layer. The model was used to estimate the rate constant of exchangeable sorption from laboratory leaching of intact rock samples. The isotopic exchange/layer diffusion model is consistent with isotopic analyses of fracturelining manganese oxides, which are thicker and exhibit strongly ratelimited interaction with U in fracture waters.
REFERENCES