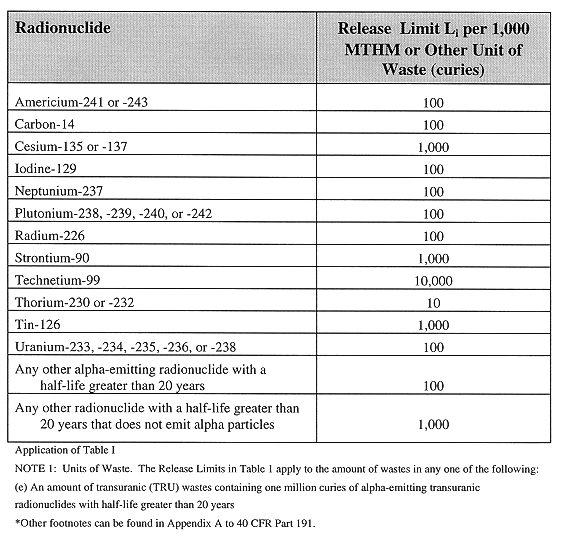
Table I Release Limits for the Containment Requirements (EPA 1994,
Appendix A, Table I)
Hong-Nian Jow, D. R. Anderson and Mel Marietta
Sandia
National Laboratories
Albuquerque, New Mexico 87185-1328
Jon Helton
Department of Mathematics
Arizona State
University
Tempe, Arizona 85287-1804
George Basabilvazo
U.S. Department of Energy
Carlsbad, New Mexico, 87220
ABSTRACT
This paper presents an overview of the methodology used in the recent performance assessment (PA) to support the U.S. Department of Energy (DOE) Carlsbad Area Offices (CAOs) Waste Isolation Pilot Plant (WIPP) Compliance Certification Application (CCA). The results of this recently completed WIPP PA will be presented. Major release modes contributing to the total radionuclide release to the accessible environment will be discussed. Comparison of the mean complementary cumulative distribution function (CCDF) curve against the Environmental Protection Agency (EPA) radionuclide release limits will be presented.
INTRODUCTION
The WIPP site is located in southeastern New Mexico and is being developed by the DOE for the safe geological disposal of transuranic (TRU) radioactive waste. The WIPP must comply with various EPA regulations, including 40 CFR 191, Subpart B, Environmental Radiation Protection Standards for the Management and Disposal of Spent Nuclear Fuel, High-Level and Transuranic Radioactive Wastes and 40 CFR 194, Criteria for the Certification and Re-Certification of the Waste Isolation Pilot Plants Compliance With the 40 CFR Part 191 Disposal Regulations.
The Sandia National Laboratories (SNL) WIPP project has been providing scientific research and development support to the DOE during the last two decades, including development of computer codes for PA. These include computer codes to simulate the repository system after operation, transport and retardation of radionuclides, and other hazardous materials from the repository through different hydrogeologic formations, and simulation of possible radionuclide releases due to future human intrusion into the repository. PA presents the results of the most probable outcomes of a disposal system for 10,000 years and compares the calculated radionuclide releases to probabilistic radionuclide release limits prescribed in section 191.13 of 40 CFR 191. The SNL WIPP project has done preliminary performance assessments inthe past several years (1,2). The results of the 1996 WIPP performance assessment are used to support the CCA for the WIPP repository.
CONTAINMENT REQUIREMENT OF 40 CFR 191
The EPA, in 40 CFR Part 191 (3), specifies the generally applicable radiation standards for the protection of public health and the environment for the disposal of TRU and high-level radioactive wastes. The complete text of the 40 CFR § 191.13(a) Containment Requirements follows:
Disposal systems for spent nuclear fuel or high-level or transuranic radioactive wastes shall be designed to provide a reasonable expectation, based on performance assessments, that the cumulative releases of radionuclides to the accessible environment for 10,000 years after disposal from all significant processes and events that may affect the disposal system shall:
- Have a likelihood of less than one chance in 10 of exceeding the quantities calculated according to Table I (Appendix A); and
- Have a likelihood of less than one chance in 1,000 of exceeding ten times the quantities calculated according to Table I (Appendix A).
Table I Release Limits for the Containment Requirements (EPA 1994,
Appendix A, Table I)

For a release to the accessible environment that involves a mix of radionuclides, the limits in Table I are used to determine a normalized release (nR) of radionuclides for comparison with the release limits
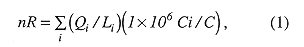
where
Qi = cumulative release in curies (Ci) of radionuclide i into the accessible environment during the 10,000-year period following closure of the repository. Li = release limit in curies for radionuclide i given in Table I. C = amount of curies of TRU waste emplaced in the repository. (TRU wastes contain alpha-emitting transuranic radionuclides with half-lives greater than 20 years.)
As indicated in Note 1(e) to Table I in Appendix A of 40 CFR Part 191, the "other unit of waste" for TRU waste shall be "an amount of transuranic wastes containing 1 million curies of alpha-emitting transuranic radionuclides with half-lives greater than 20 years."
PERFORMANCE ASSESSMENT METHODOLOGY
PAs are the basis for addressing the EPA containment requirements. 40 CFR § 191.12 defines performance as follows:
"Performance assessment" means an analysis that: 1) identifies the processes and events that might affect the disposal system; 2) examines the effects of these processes and events on the performance of the disposal system; and 3) estimates the cumulative releases of radionuclides, considering the associated uncertainties, caused by all significant processes and events.
The calculation of the probabilities and consequences of future occurrences begins with the determination of the scenarios to be analyzed. Scenarios are determined through a formal process similar to that proposed by Cranwell et al. (4). This process has four steps:
Once scenarios have been defined, a calculational methodology for evaluating their consequences must be developed. The calculational methodology must address stochastic uncertainty related to aggregation and stochastic variation, and subjective uncertainty because of, for example, measurement difficulties or unknowable data.
CHARACTERIZATION OF UNCERTAINTY IN RISK
For practical purposes, the calculation of risk for this performance assessment is separated into two components: 1) due to stochastic uncertainty, represented in an individual CCDF, and 2) due to subjective uncertainty, which is represented by the family of CCDFs. This can be represented mathematically as a double sum, presented here in a stylized form for clarity,
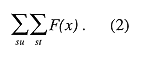
Here, F(x) is a procedure for estimating the normalized release to the accessible environment associated with each scenario that could occur at the WIPP site.
The inner sum denoted with the subscript st is a probabilistic characterization of the uncertainty associated with parameters used to characterize stochastic uncertainty. For example, the stochastic uncertainty may be the uncertainty in the number and time of human intrusion boreholes. It is the evaluation of F(x) through the inner sum that develops an individual CCDF. The outer sum denoted with the subscript su is a probabilistic characterization of the uncertainty associated with parameters used to characterize subjective uncertainty. Subjective uncertainty results from measurement uncertainty or unknowable data. It is the combined evaluation in the outer sum of the inner sum with F(x) that develops the family of CCDFs.
Techniques for Probabilistic Analysis
Monte Carlo analysis is the general name for the probabilistic techniques used to evaluate the double sum discussed above.
Within the general framework of Monte Carlo analysis, PA uses two methods for generating the samples propagated through the model system. One method (Latin hypercube sampling) is used for the assessment of subjective uncertainty, and another method (random sampling) is used for the characterization of stochastic uncertainty.
Information about the ranges and distributions of possible input parameter values can be drawn from a variety of sources, including field data, laboratory data, and literature. A review process leads from the available data to the construction of the distribution functions used in the performance assessment to characterize uncertainty in input parameters. The outcome of the review process is a cumulative distribution function (CDF) D(x) for each independent variable of interest.
Latin hypercube sampling (LHS), in which the full range of each variable is subdivided into intervals of equal probability and samples are drawn from each interval, is then used to select values of uncertain parameters associated with the physical system being simulated. Vectors (sets) of parameter values are created from the uncertain variables in the database by LHS of each variable for the set of simulations comprising a performance assessment of the system. In this PA, 57 parameters are sampled using LHS, and 100 vectors are assembled. Each of the fixed parameter values from the database and a vector of sampled parameter values are combined to form a realization (a set of input parameters). Each realization is then propagated through the performance assessment codes (see later section). This sampling is used for parameters that are evaluated in the outer sum of the double sum
Random sampling of the occurrence of possible future events is used to generate the possible futures (probabilistic futures) that comprise a CCDF. This sampling is used to select values of uncertain parameters associated with future human activities, or in other words, it is used to incorporate stochastic uncertainty into the WIPP PA. This sampling is used for parameters evaluated in the inner sum of the double sum.
COMPUTER CODES USED IN PERFORMANCE ASSESSMENT
To evaluate scenario consequences for both undisturbed and disturbed (i.e., human intrusion events) performance, computer codes are used to simulate relevant features of the disposal system. The flow of information and primary roles of the codes used are discussed in this section. Parameter values and disposal system conditions must be passed between codes several times in an assessment.
The codes are executed under the requirements of the software configuration management system (SCMS), which creates and maintains a complete record of the input data and results of each calculation, together with the exact codes used to create those results. For this application, PA codes used in conjunction with LHS or random sampling were executed under the SCMS.
Figure 1 shows a method of visualizing how the various performance assessment codes relate to each other and to the estimation of scenario consequences. This figure represents a vertical cross section of the disposal system, associating the major codes with the particular components of the system each code simulates. As shown in the figure, BRAGFLO, SANTOS, NUTS, and PANEL address the Salado. GRASP-INV, SECOFL2D, and SECOTP2D address the Culebra. CUTTINGS_S, BRAGFLO_DBR, and PANEL address the immediate consequences of inadvertent human intrusion through one or more exploratory boreholes.
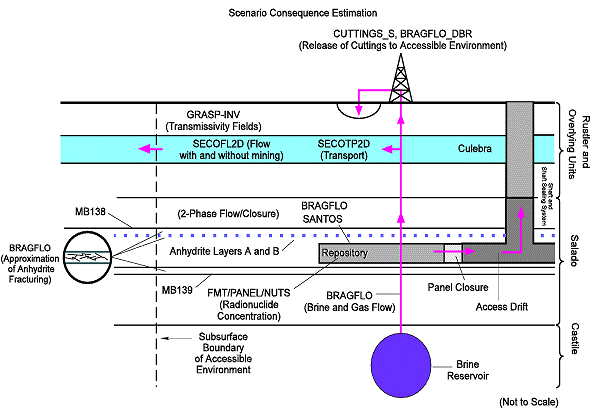
Fig. 1. Schematic side view of the
disposal system associating performance assessment codes with the components of
the disposal system each code simulates.
The computer code CCDFGF is used to 1) determine random sequences of future events that may occur over the next 10,000 years at the WIPP site; 2) estimate the radionuclide releases resulting for these random sequences of future events, using the results of the calculations described in this section; and 3) construct a CCDF for each realization.
SUMMARY OF PERFORMANCE ASSESSMENT RESULTS
For the undisturbed performance, the PA results show that the quantity of actinides that may reach the accessible environment boundary through the anhydrite interbeds is insignificant and has no effect on the compliance determination. No migration of radionuclides is expected to occur vertically through the Salado or through the shaft seal system. The following discussion is for the disturbed performance.
Each CCDF is calculated for a single LHS vector of input parameters and is conditional on the occurrence of that particular combination of parameter values. Multiple realizations of the PA calculations yield a family of CCDFs in which each individual CCDF is generated from a different LHS vector. Families of CCDFs calculated for the WIPP PA are based on 100 LHS vectors drawn from distributions of values for 57 imprecisely known parameters. Mean and percentile CCDFs are constructed from families and provide summary measures of disposal system performance.
To demonstrate convergence of the mean and to address the associated criteria of 40 CFR Part 194, an operational approach of multiple replication as proposed by Iman (5) is used for this PA. The complete set of PA calculations was repeated three times with all aspects of the analysis identical except for the random seed used to initiate the LHS procedure. This technique of multiple replication allows evaluation of the adequacy of the sample size chosen in the Monte Carlo analysis and provides a suitable measure of confidence in the estimate of the mean CCDF used to demonstrate compliance with 40 CFR § 191.13(a).
A family of CCDFs for one of the three replicates is shown in Fig. 2. The figure contains 100 CCDFs. The families of CCDFs for the other two replicates are similar to Fig. 2. All CCDFs of three replicates lie below and to the left of the limits specified in 40 CFR § 191.13(a).
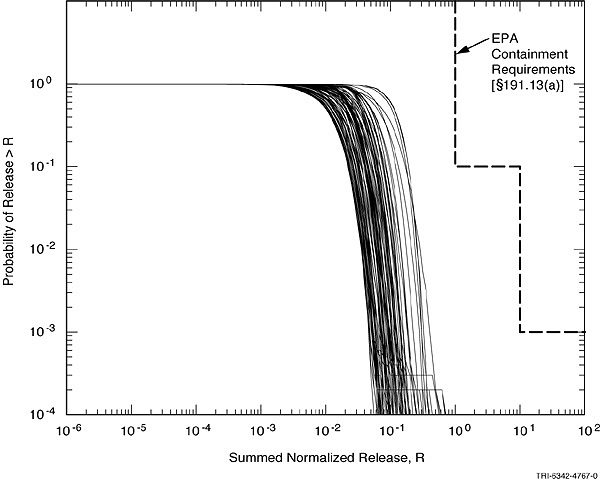
Fig. 2. Distribution of CCDFs for
normalized radionuclide releases to the accessible environment from the WIPP,
replicate 1.
Quantitative verification of the similarity of the three replicates is demonstrated in Fig. 3, which shows the mean CCDFs calculated for each of the three replicates, together with an overall mean CCDF that is the arithmetic mean of the three individual mean CCDFs. Figure 3 demonstrates two key points. First, the overall mean CCDF lies entirely below and to the left of the limits specified in 40 CFR ' 191.13(a). Thus, the WIPP is in compliance with the containment requirements of 40 CFR Part 191. Second, the sample size of 100 in each replicate is sufficient to generate a stable distribution of outcomes.
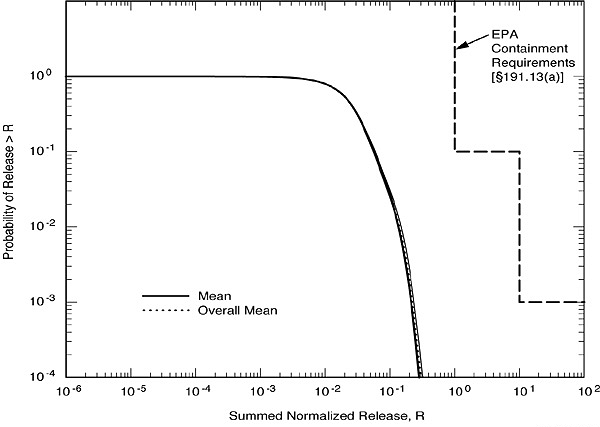
Fig. 3. Mean CCDFs for normalized
radionuclide releases to the accessible environment.
Release Modes Contributing to the Total Radionuclide Release
Radionuclide releases to the accessible environment can be grouped into four categories according to their mode of release:
Each of these four modes has the potential to contribute to the total quantity of radionuclides released from the repository, and therefore each has the potential to affect the position of the mean CCDF.
Figure 4 provides a display of the relative contribution of each mode to the total release. Releases for each of the three replicates are similar, and results are shown for replicate 1 only for simplicity. Mean CCDFs are shown for the total normalized release and for the normalized releases resulting from cuttings and cavings, spallings, and direct brine release. The mean CCDF for subsurface releases resulting from groundwater transport is not shown because those releases were less than 10-6 EPA units and the CCDF cannot be shown at the scale of this figure. Releases from cuttings and cavings are shown to be the most important contributors to the location of mean CCDF, with spallings also making a small contribution. Direct brine releases are less important, and have very little effect on the location of the mean.
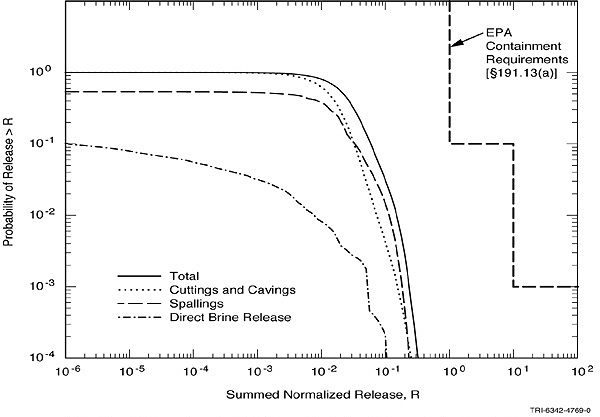
Fig. 4. Mean CCDFs for specific
release modes, replicate 1.
REFERENCES